
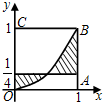
 如图,正方形OABC的边长为1,记曲线y=x2和直线$y=\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)为Ω,若向正方形OABC内任意投一点M,则点M落在区域Ω内的概率为( )
如图,正方形OABC的边长为1,记曲线y=x2和直线$y=\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)为Ω,若向正方形OABC内任意投一点M,则点M落在区域Ω内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
分析 欲求所投的点落在阴影部分内部的概率,须结合定积分计算阴影部分平面区域的面积,再根据几何概型概率计算公式易求解
解答 解:根据题意,正方形OABC的面积为1×1=1,
而阴影部分的面积为${∫}_{0}^{\frac{1}{2}}(\frac{1}{4}-{x}^{2})dx+{∫}_{\frac{1}{2}}^{1}({x}^{2}-\frac{1}{4})dx$=($\frac{1}{4}x-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{\frac{1}{2}}$+($\frac{1}{3}{x}^{3}-\frac{1}{4}x$)|${\;}_{\frac{1}{2}}^{1}$=$\frac{1}{4}$,
由几何概型公式得到,向正方形OABC中任取一点M,点M取自阴影部分的概率$\frac{\frac{1}{4}}{1}=\frac{1}{4}$;
故选A.
点评 本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{31}{16}$ | B. | $\frac{31}{32}$ | C. | 31 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正 | B. | 负 | C. | 非负 | D. | 非正 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com