Question

15．在直三棱柱ABC-A₁B₁C₁中，AA₁=AC，AB⊥AC，求证：A₁C⊥BC₁．

Answer 1

分析 连接AC₁，根据AA₁=AC可得到A₁C⊥AC₁，而根据线面垂直的判定定理AB⊥平面ACC₁A₁，从而得到A₁C⊥AB，所以根据线面垂直的判定定理可得到A₁C⊥平面ABC₁，所以A₁C⊥BC₁．

解答 证明：如图，连接AC₁；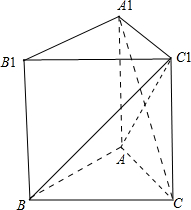
AA₁=AC；
∴四边形ACC₁A₁是菱形；
∴A₁C⊥AC₁；
AA₁⊥底面ABC，AB?底面ABC；
∴AA₁⊥AB，即AB⊥AA₁；
又AB⊥AC；C₁A₁
∴AB⊥平面ACC₁A₁，A₁C?平面ACC₁A₁
∴AB⊥A₁C，即A₁C⊥AB，AB∩AC₁=A；
∴A₁C⊥平面ABC₁，BC₁?平面ABC₁；
∴A₁C⊥BC₁．

点评 考查要证明线线垂直可转化为证明线面垂直，以及菱形的定义，菱形对角线的特点，直棱柱的侧棱和底面的关系，线面垂直的判定定理．