
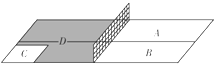
 乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:
乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:分析 (1)记Ai为事件“小明对落点在A上的来球回球的得分为i分”,
Bi为事件“小明对落点在B上的来球回球的得分为i分”,
D为事件“小明两次回球的落点中恰有1次的落点在乙上”;
计算对应的概率值,求出小明两次回球的落点中恰有1次的落点在乙上的概率;
(2)由题意随机变量ξ可能的取值为0、1、2、3、4、6,
由事件的独立性和互斥性,计算对应的概率,写出ξ的分布列,计算数学期望Eξ.
解答 解:(1)记Ai为事件“小明对落点在A上的来球回球的得分为i分”(i=0,1,3),
则P(A3)=$\frac{1}{2}$,P(A1)=$\frac{1}{3}$,
P(A0)=1-$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$;
记Bi为事件“小明对落点在B上的来球回球的得分为i分”(i=0,1,3),
则P(B3)=$\frac{1}{5}$,P(B1)=$\frac{3}{5}$,
P(B0)=1-$\frac{1}{5}$-$\frac{3}{5}$=$\frac{1}{5}$;
记D为事件“小明两次回球的落点中恰有1次的落点在乙上”,
由题意,D=A3B0+A1B0+A0B1+A0B3,
由事件的独立性和互斥性,
P(D)=P(A3B0+A1B0+A0B1+A0B3)
=P(A3B0)+P(A1B0)+P(A0B1)+P(A0B3)
=P(A3)P(B0)+P(A1)P(B0)+P(A0)P(B1)+P(A0)P(B3)
=$\frac{1}{2}$×$\frac{1}{5}$+$\frac{1}{3}$×$\frac{1}{5}$+$\frac{1}{6}$×$\frac{3}{5}$+$\frac{1}{6}$×$\frac{1}{5}$=$\frac{3}{10}$,
所以小明两次回球的落点中恰有1次的落点在乙上的概率为$\frac{3}{10}$;
(2)由题意,随机变量ξ可能的取值为0、1、2、3、4、6,
由事件的独立性和互斥性,得
P(ξ=0)=P(A0B0)=$\frac{1}{6}$×$\frac{1}{5}$=$\frac{1}{30}$,
P(ξ=1)=P(A1B0+A0B1)=P(A1B0)+P(A0B1)
=$\frac{1}{3}$×$\frac{1}{5}$+$\frac{1}{6}$×$\frac{3}{5}$=$\frac{1}{6}$,
P(ξ=2)=P(A1B1)=$\frac{1}{3}$×$\frac{3}{5}$=$\frac{1}{5}$,
P(ξ=3)=P(A3B0+A0B3)=P(A3B0)+P(A0B3)
=$\frac{1}{2}$×$\frac{1}{5}$+$\frac{1}{5}$×$\frac{1}{6}$=$\frac{2}{15}$,
P(ξ=4)=P(A3B1+A1B3)=P(A3B1)+P(A1B3)=$\frac{1}{2}$×$\frac{3}{5}$+$\frac{1}{3}$×$\frac{1}{5}$=$\frac{11}{30}$,
P(ξ=6)=P(A3B3)=$\frac{1}{2}$×$\frac{1}{5}$=$\frac{1}{10}$.
可得随机变量ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | 6 |
| P | $\frac{1}{30}$ | $\frac{1}{6}$ | $\frac{1}{5}$ | $\frac{2}{15}$ | $\frac{11}{30}$ | $\frac{1}{10}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,也考查了相互独立事件的概率计算问题,是综合题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
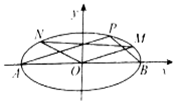 如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.
如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
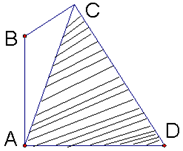 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com