
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
分析 根据C,F,D三点共线可得x,y的关系,再利用基本不等式解出.
解答 解:$\overrightarrow{AF}=x\overrightarrow{AB}+y\overrightarrow{AC}=2x\overrightarrow{AD}+y\overrightarrow{AC}$,
因为C,F,D三点共线,
所以2x+y=1且x>0,y>0,
则$\frac{1}{x}+\frac{2}{y}=({\frac{1}{x}+\frac{2}{y}})(2x+y)=4+\frac{y}{x}+\frac{4x}{y}≥4+2\sqrt{\frac{y}{x}\;•\;\frac{4x}{y}}=8$,
当且仅当$\frac{y}{x}=\frac{4x}{y}$,即$x=\frac{1}{4}$,$y=\frac{1}{2}$时,上式取等号,
故$\frac{1}{x}+\frac{2}{y}$有最小值8,
故选D.
点评 本题考查了向量共线定理和基本不等式的性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
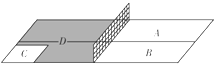 乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:
乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{25}$ | B. | $-\frac{18}{25}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com