
分析 由题意,P在原点时,||PF1|-|PF2||=0,求出F2(5,0)关于直线y=$\frac{3}{4}$x对称点的坐标,可得||PF1|-|PF2||的最大值,即可求出||PF1|-|PF2||的取值范围.
解答 解:由题意,P在原点时,||PF1|-|PF2||=0,
F2(5,0)关于直线y=$\frac{3}{4}$x对称点的坐标为F(a,b),则$\left\{\begin{array}{l}{\frac{b}{a-5}•\frac{3}{4}=-1}\\{\frac{b}{2}=\frac{3}{4}•\frac{a+5}{2}}\end{array}\right.$,∴a=$\frac{9}{5}$,b=$\frac{51}{10}$,
∴||PF1|-|PF2||的最大值为$\sqrt{(\frac{9}{5}+5)^{2}+(\frac{51}{10})^{2}}$=8.5,
∴||PF1|-|PF2||的取值范围为[0,8.5].
故答案为:[0,8.5].
点评 本题考查||PF1|-|PF2||的取值范围,考查对称性的运用,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
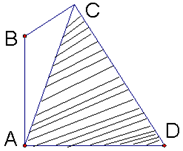 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com