
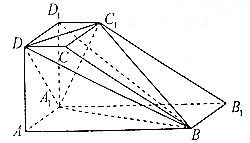
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.分析 (Ⅰ)连接AD1,B1D1,证明A1D⊥BD1,A1C1⊥BD1,即可证明:BD1⊥平面A1C1D;
(Ⅱ)建立坐标系,求出平面的法向量,即可求BD1与平面A1BC1所成角的正弦值.
解答 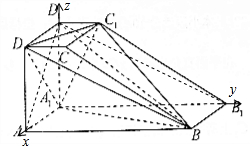 (Ⅰ)证明:连接AD1,B1D1,则AB是平面AD1的垂线,BD1是平面AD1的斜线,AD1是BD1在平面AD1内的射影,∴A1D⊥BD1,
(Ⅰ)证明:连接AD1,B1D1,则AB是平面AD1的垂线,BD1是平面AD1的斜线,AD1是BD1在平面AD1内的射影,∴A1D⊥BD1,
∵Rt△C1D1A1∽Rt△B1A1D1,∴∠D1A1C1+∠A1D1B1=∠D1A1C1+∠D1C1A1=90°,∴A1C1⊥B1D1,∴A1C1⊥BD1,
∵A1D∩A1C1=A1,
∴BD1⊥平面A1C1D;
(Ⅱ)解:建立如图所示的坐标系,则A1(0,0,0),B(2,4,0),C1(0,1,2),D1(0,0,2),
$\overrightarrow{{A}_{1}B}$=(2,4,0),$\overrightarrow{{A}_{1}{C}_{1}}$=(0,1,2),$\overrightarrow{B{D}_{1}}$=(-2,-4,2),
设BD1与平面A1BC1所成角为θ,平面A1BC1的一个法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{2x+4y=0}\\{y+2z=0}\end{array}\right.$,取$\overrightarrow{n}$=(4,-2,1),
则sinθ=|$\frac{2}{\sqrt{24}•\sqrt{21}}$=$\frac{\sqrt{14}}{42}$.
点评 本题考查线面垂直的证明,考查线面角,考查向量方法的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|x<1或x>3} | C. | {x|0<x<1} | D. | {x|x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 170石 | B. | 180石 | C. | 190石 | D. | 200石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
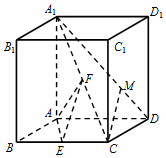 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
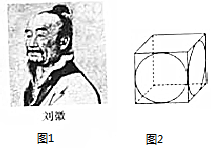 我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )| A. |  | B. | 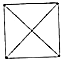 | C. | 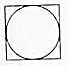 | D. | 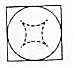 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com