
分析 由2b,|$\overrightarrow{{F}_{1}{F}_{2}}$|,2a成等差数列得到一个关于a,b,c的方程,再由△PF1F2的面积为12得到另一方程,结合隐含条件求得a,b的值得答案.
解答 解:由题意知,2a+2b=2|F1F2|=4c,
${S}_{△P{F}_{1}{F}_{2}}=\frac{1}{2}|{F}_{1}{F}_{2}|•b=bc=12$,
∴a=2c-b,又a2=b2+c2,
∴(2c-b)2=b2+c2,解得:c=4.
∴b=3,a=5.
∴椭圆C的方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$.
故答案为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$.
点评 本题考查椭圆的简单性质,考查了椭圆标准方程的求法,是基础题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$) | B. | (-∞,-1) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
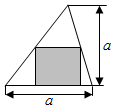 在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )
在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-l | B. | e | C. | 3 | D. | e+l |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com