Question

20．若复数t=$\frac{2}{（1-i）^{2}}$+$\frac{3+i}{1-i}$的虚部为m，函数f（x）=x+$\frac{4}{x-1}$+1，（x∈{2，3}）的最小值为n．
（1）求m，n的值；
（2）如图，一个圆锥的底面半径为m，高为n，在其中有一个半径为x的内接圆柱，当x为何值时，圆柱的侧面积最大，最大值是多少？

Answer 1

分析 （1）由复数代数形式的乘除运算化简求得m，利用基本不等式求最值求得n；
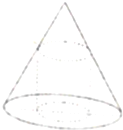
（2）把圆锥内接圆柱的母线用x表示，写出圆柱的表面积，转化二次函数求最值．

解答 解：（1）由t=$\frac{2}{（1-i）^{2}}$+$\frac{3+i}{1-i}$=$\frac{2}{-2i}+\frac{3+i}{1-i}=\frac{1}{-i}+\frac{3+i}{1-i}=i+\frac{（3+i）（1+i）}{（1-i）（1+i）}$=$i+\frac{2+4i}{2}=1+3i$，
则m=3，
又x∈{2，3}，故f（x）=x+$\frac{4}{x-1}$+1=x-1+$\frac{4}{x-1}+2≥2\sqrt{（x-1）•\frac{4}{x-1}}+2=6$，
即当x=3时，f（x）的最小值为6，即n=6．
（2）设圆锥内接圆柱的母线长为l，则：$\frac{x}{3}=\frac{6-l}{6}$，即l=6-2x（0＜x＜3），
则圆柱的侧面积S=2πxl=2πx（6-2x）=-4πx²+12πx．
当x=$\frac{3}{2}$时，S有最大值为9π．

点评 本题考查复数代数形式的乘除运算，考查了函数值域的求法，训练了柱锥台体的表面积的求法，是中档题．