已知$f(x)=2sin$.则“?x∈R.f 是“ω=2 的( )A．充分必要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

16．已知$f（x）=2sin（ωx-\frac{π}{3}）$，则“?x∈R，f（x+π）=f（x）”是“ω=2”的（　　）

	A．	充分必要条件		B．	充分不必要条件
	C．	必要不充分条件		D．	既不充分也不必要条件

分析由ω=2，可得f（x）=2sin$（2x-\frac{π}{3}）$，可得f（x+π）=f（x）．反之不成立，例如ω=4也成立．即可判断出结论．

解答解：由ω=2，可得f（x）=2sin$（2x-\frac{π}{3}）$，∴f（x+π）=f（x）．
反之不成立，例如ω=4也成立．
∴“?x∈R，f（x+π）=f（x）”是“ω=2”的必要不充分条件．
故选：C．

点评本题考查了三角函数的图象与性质、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

6．已知$a=\sqrt{3}$，$b={125^{\frac{1}{6}}}$，$c={log_{\frac{1}{6}}}\frac{1}{7}$，则下列不等关系正确的是（　　）

A．

b＜a＜c

B．

a＜b＜c

C．

b＜c＜a

D．

c＜a＜b

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．设变量x，y满足约束条件$\left\{\begin{array}{l}{2x-y-1≥0}\\{x-3y+2≤0}\\{x+2y-8≤0}\end{array}\right.$，则目标函数z=（2-z）x+y的最大值为（　　）

A．

$\frac{3}{2}$

B．

C．

$\frac{7}{3}$

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．袋中有外观相同的红球，黑球各1个，现依次有放回地随机摸取3次，每次摸取1个球，若摸到红球时得2分，摸到黑球时得1分，则3次摸球所得总分为5的概率为（　　）

A．

$\frac{5}{7}$

B．

$\frac{6}{7}$

C．

$\frac{3}{8}$

D．

$\frac{5}{8}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．在△ABC中，内角A、B、C的对边分别是a，b，c，若λsinA=sinB+sinC（λ∈R）．
（Ⅰ）当λ=3，且b=c时，求cosA的值；
（Ⅱ）当A=60°时，求λ的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．在△ABC中，若a=1，∠A=$\frac{π}{4}$，则$\frac{{\sqrt{2}b}}{sinC+cosC}$=$\sqrt{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．

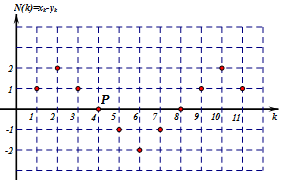已知一个由11人组成的评审委员会以投票方式从符合要求的甲，乙两名候选人中选出一人参加一次活动．投票要求委员会每人只能选一人且不能弃选，每位委员投票不受他人影响．投票结果由一人唱票，一人统计投票结果．
（Ⅰ）设：在唱到第k张票时，甲，乙两人的得票数分别为x_k，y_k，N（k）=x_k-y_k，k=1，2，…，11．若下图为根据一次唱票过程绘制的N（k）图，
则根据所给图表，在这次选举中获胜方是谁？y₇的值为多少？图中点P提供了什么投票信息？
（Ⅱ）设事件A为“候选人甲比乙恰多3票胜出”，假定每人选甲或乙的概率皆为$\frac{1}{2}$，则事件A发生的概率为多少？
（Ⅲ）若在不了解唱票过程的情况下已知候选人甲比乙3票胜出．则在唱票过程中出现甲乙两人得票数相同情况的概率是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

5．已知抛物线y²=2px（p＞0）的准线为l，若l与圆x²+y²+6x+5=0的交点为A，B，且|AB|=2$\sqrt{3}$．则p的值为4或8．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．把函数f（x）=cos（2x+φ）的图象上所有的点向左平移$\frac{π}{6}$个单位长度后得到y=g（x）的图象，若y=g（x）的一个对称中心是（$\frac{π}{6}$，0），则φ的一个可能取值是（　　）

A．

$\frac{π}{3}$

B．

$\frac{7π}{12}$

C．

$\frac{5π}{6}$