
(本小题满分14分)已知A,B分别是直线y=x和y=-x上的两个动点,线段AB的长为2 ,D是AB的中点.
,D是AB的中点.
(Ⅰ)求动点D的轨迹C的方程;
(Ⅱ)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
① 当|PQ|=3时,求直线l的方程;
② 试问在x轴上是否存在点E(m,0),使 ·
·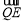 恒为定值?若存在,求出E点的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E点的坐标及定值;若不存在,请说明理由.
(Ⅰ)x2+y2=3;(Ⅱ)﹣2 .
【解析】
试题分析:(Ⅰ)设 ,然后根据线段AB的长为
,然后根据线段AB的长为 ,D是AB的中点消去a与b,得到x与y的等量关系,即为动点D的轨迹C的方程;
,D是AB的中点消去a与b,得到x与y的等量关系,即为动点D的轨迹C的方程;
(Ⅱ)①讨论直线l与x轴是否垂直,然后利用点到直线的距离公式建立等式关系,从而求出直线方程;
②讨论直线l的斜率是否存在,不存在时直接求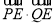 ,存在时,将直线与圆联立方程组,消去y,然后设
,存在时,将直线与圆联立方程组,消去y,然后设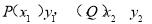 ,将
,将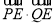 表示出来,使其与k无关即可求出m的值.
表示出来,使其与k无关即可求出m的值.
试题解析:
【解析】
(Ⅰ)设 ,
,
∵D是AB的中点,∴x= ,y=
,y=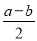 ,
,
∵|AB|= ,∴(a﹣b)2+(a+b)2=12,
,∴(a﹣b)2+(a+b)2=12,
∴(2y)2+(2x)2=12,∴点D的轨迹C的方程为x2+y2=3.
(Ⅱ)①当直线l与x轴垂直时,P(1,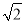 ),Q(1,﹣
),Q(1,﹣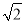 ),此时|PQ|=2
),此时|PQ|=2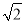 ,不符合题意;
,不符合题意;
当直线l与x轴不垂直时,设直线l的方程为y=k(x﹣1),由于|PQ|=3,所以圆心C到直线l的距离为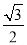 ,
,
由 =
=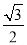 ,解得k=±
,解得k=±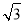 .故直线l的方程为y=±
.故直线l的方程为y=±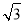 (x﹣1).
(x﹣1).
②当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x﹣1),
由消去y得(k2+1)x2﹣2k2x+k2﹣3=0,
设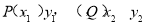 则由韦达定理得
则由韦达定理得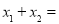
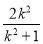 ,
,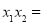
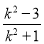 ,
,
则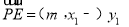 ,
, 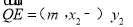 ,
,
∴

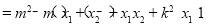
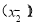
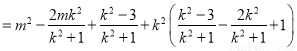

要使上式为定值须 ,解得m=1,∴
,解得m=1,∴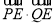 为定值﹣2,
为定值﹣2,
当直线l的斜率不存在时P(1,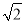 ),Q(1,﹣
),Q(1,﹣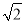 ),
),
由E(1,0)可得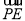 =(0,﹣
=(0,﹣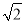 ),
),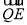 =(0,
=(0,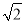 ),
),
∴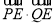 =﹣2,
=﹣2,
综上所述当E(1,0)时,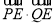 为定值﹣2.
为定值﹣2.
考点:①向量在几何中的应用;②轨迹问题和直线和圆的方程的应用;③转化的思想和计算的能力.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试文科数学试卷(解析版) 题型:填空题
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是________.
(把你认为正确的结论都填上)
①BD∥平面CB1D1;
②AC1⊥平面CB1D1;
③AC1与底面ABCD所成角的正切值是;
④二面角C—B1D1-C1的正切值是;
⑤过点A1与异面直线AD与CB1成70°角的直线有2条.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com