Question

7．已知P是直线3x+4y-10=0上的动点，PA，PB是圆x²+y²-2x+4y+4=0的两条切线，A，B是切点，C是圆心，那么四边形PACB面积的最小值为2$\sqrt{2}$．

Answer 1

分析 S_{四边形PACB}=S_△PAC+S_△PBC，当|PC|取最小值时，|PA|=|PB|取最小值，即S_△PAC=S_△PBC取最小值，由此能够求出四边形PACB面积的最小值．

解答 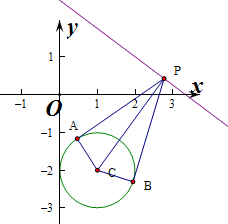解：圆的标准方程为（x-1）²+（y+2）²=1，
则圆心为C（1，-2），半径为1，
则直线与圆相离，如图，S四边形_PACB=S_△PAC+S_△PBC
而S_△PAC=$\frac{1}{2}$|PA|•|CA|=$\frac{1}{2}$|PA|，
S_△PBC=$\frac{1}{2}$|PB|•|CB|=$\frac{1}{2}$|PB|，
又|PA|=$\sqrt{|PC{|}^{2}-1}$，|PB|=$\sqrt{|PC{|}^{2}-1}$，
∴当|PC|取最小值时，|PA|=|PB|取最小值，
即S_△PAC=S_△PBC取最小值，此时，CP⊥l，
|CP|=$\frac{|3-2×4-10|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{15}{5}=3$，则|PA|=$\sqrt{{3}^{2}-1}=\sqrt{8}$=2$\sqrt{2}$，
则S_△PAC=S_△PBC=$\frac{1}{2}$×2$\sqrt{2}$×1=$\sqrt{2}$，
即四边形PACB面积的最小值是2$\sqrt{2}$．
故答案为：2$\sqrt{2}$

点评 本题考查直线和圆的位置关系，解题时要认真审题，在解答过程中要合理地运用数形结合思想．