
 .
. 分析 由已知及诱导公式可求sin$\frac{23π}{5}$=cos$\frac{π}{10}$,cos(-$\frac{17π}{4}$)=cos$\frac{π}{4}$,结合0<$\frac{π}{10}$<$\frac{π}{4}$<$\frac{π}{2}$,由余弦函数的单调性即可比较大小.
解答 解:∵sin$\frac{23π}{5}$=sin(4π+$\frac{3π}{5}$)=sin($\frac{π}{2}$-$\frac{π}{10}$)=cos$\frac{π}{10}$,
cos(-$\frac{17π}{4}$)=cos(4π+$\frac{π}{4}$)=cos$\frac{π}{4}$,
又∵0<$\frac{π}{10}$<$\frac{π}{4}$<$\frac{π}{2}$,y=cosx在(0,$\frac{π}{2}$)上单调递减,
∴cos$\frac{π}{10}$>cos$\frac{π}{4}$,即sin$\frac{23π}{5}$>cos(-$\frac{17π}{4}$).
故答案为:sin$\frac{23π}{5}$>cos(-$\frac{17π}{4}$).
点评 本题主要考查了诱导公式,余弦函数的单调性的综合应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题

| A. | 0<f'(3)<f'(4)<f(4)-f(3) | B. | 0<f(4)-f(3)<f'(3)<f'(4) | C. | 0<f'(4)<f'(3)<f(4)-f(3) | D. | 0<f'(4)<f(4)-f(3)<f'(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16f(-3)>9f(4) | B. | 16f(3)<9f(-4) | C. | 9f(3)>16f(4) | D. | 9f(-3)<16f(-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )| A. |  | B. |  | C. |  | D. | 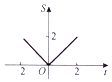 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com