
分析 化简集合A、B,求出∁RB与A∩(∁RB)即可.
解答 解:∵集合A={x|y=$\frac{1}{x-1}$+ln(x+3)}
={x|$\left\{\begin{array}{l}{x-1≠0}\\{x+3>0}\end{array}\right.$}
={x|x>-3且x≠1}
=(-3,1)∪(1,+∞),
B={y|y=lg(2x-x2)}
={y|y=lg[-(x-1)2+1]}
={y|y≤0}
=(-∞,0];
∴∁RB=(0,+∞),
∴A∩(∁RB)=(0,1)∪(1,+∞).
故答案为:(0,1)∪(1,+∞).
点评 本题考查了集合的化简与运算问题,也考查了求函数的定义域和值域的应用问题,是基础题目.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
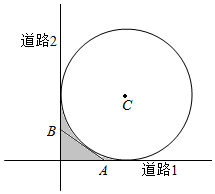 如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com