
分析 本题考查的知识点是几何概型的意义,关键是要找出方程 $\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆时(m,n)点对应的平面图形的面积大小和区间[1,6]和[2,4]分别各取一个数(m,n)点对应的平面图形的面积大小,并将他们一齐代入几何概型计算公式进行求解.
解答 解:若方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆,则m>n
在区间[1,6]和[2,4]上分别各取一个数,记为m和n,其面积为5×2=10,
满足m>n图形的面积为$\frac{(2+4)×2}{2}$=6
则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率P=$\frac{6}{10}$=$\frac{3}{5}$,
故答案为$\frac{3}{5}$.
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
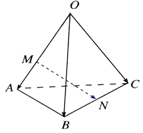
| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 8个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com