
���� ���������Ҷ��������жϣ�
������ż�����Ķ�������ʽ����жϣ�
�۸��ݵȱ����е����ʽ����жϣ�
�ܸ��ݻ�������ʽ���������������жϣ�
�ݸ��ݵȲ����е����ʽ����жϣ�
��� �⣺�١�ABC�У���$\frac{cosA}{cosB}=\frac{a}{b}$����$\frac{cosA}{cosB}=\frac{sinA}{sinB}$����tanA=tanB����A=B�������ABCһ���ǵ��������Σ��ʢ���ȷ��
�ڶ��κ���y=ax2+bx+cΪż�����ij�Ҫ������b=0����ȷ���ʢ���ȷ��
����a=b=c��������b=$\sqrt{ac}$����a��b��c���ǵȱ����У���֮������a=-1��b=-1��c=-1����a��b��c�ɵȱ����У���b=$\sqrt{ac}$��������
��$b=\sqrt{ac}��a��b��c�ɵȱȵ�$�Ȳ����Ҳ����Ҫ�������ʢ۴���
�ܡ�0��x��$\frac{��}{2}$ʱ��0��sinx��1����y=sinx+$\frac{1}{sinx}$��2�����ҽ���sinx=$\frac{1}{sinx}$����sinx=1��ȡ�úţ���sinx��1����$y=sinx+\frac{1}{sinx}��{0��x��\frac{��}{2}}��$����Сֵ��2����
�ʢܴ���
��a��b��c�ɵȲ����еij�Ҫ������2b=a+c����ȷ���ʢ���ȷ��
�ʴ�Ϊ���٢ڢ�
���� ������Ҫ�������������жϣ��漰��֪ʶ��϶࣬�ۺ��Խ�ǿ�����ѶȲ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $sin\frac{b-m}{a-m}��sin\frac{b+m}{a+m}��sin\frac{b}{a}$ | B�� | $sin\frac{b-m}{a-m}��sin\frac{b+m}{a+m}��sin\frac{b}{a}$ | ||
| C�� | $sin\frac{b-m}{a-m}��sin\frac{b}{a}��sin\frac{b+m}{a+m}$ | D�� | $sin\frac{b-m}{a-m}��sin\frac{b}{a}��sin\frac{b+m}{a+m}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{3}}}{2}$ | B�� | $\sqrt{3}$ | C�� | $2\sqrt{3}$ | D�� | $3\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
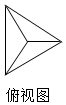 һ��������������Ϊ$\frac{2\sqrt{2}}{3}$����������ͼ�еĸ���ͼ��ͼ��ʾ����������С������ȫ�ȣ�������ͼ��һ�������Σ�����������ε�����ǣ�������
һ��������������Ϊ$\frac{2\sqrt{2}}{3}$����������ͼ�еĸ���ͼ��ͼ��ʾ����������С������ȫ�ȣ�������ͼ��һ�������Σ�����������ε�����ǣ�������| A�� | $\frac{\sqrt{6}}{3}$ | B�� | $\frac{2\sqrt{6}}{3}$ | C�� | $\frac{2\sqrt{2}}{3}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com