
| A. | $[-4,\frac{5}{4}]∪[2,+∞)$ | B. | [-4,2] | C. | $(\frac{5}{4},2]$ | D. | $[{-4,\frac{5}{4}}]$ |
分析 函数f(x)的图象与函数y=-2x+8共有两个交点,可能为:两个交点均为y=-2x+8与二次函数y=x2的交点,也可能为:两个交点为y=-2x+8与y=2x+3的交点,另一个是y=-2x+8与二次函数y=x2的交点,进而得到答案.
解答 解:y=x2与y=-2x+8共有两个交点(-4,16),(2,4),
y=2x+3与y=-2x+8有一个交点($\frac{5}{4}$,$\frac{11}{2}$),
若方程f(x)+2x-8=0恰有两个不同实根,
则函数f(x)的图象与函数y=-2x+8共有两个交点,
若两个交点均为y=-2x+8与二次函数y=x2的交点,则a≥2,
若两个交点为y=-2x+8与y=2x+3的交点,另一个是y=-2x+8与二次函数y=x2的交点,则-4≤a≤$\frac{5}{4}$,
综相所述,a∈$[-4,\frac{5}{4}]∪[2,+∞)$,
故选:A.
点评 本题考查的知识点是根的存在性及根的个数判断,分段函数的应用,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | $\frac{\sqrt{5}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{5}{2}$ | B. | $m>\frac{5}{2}$ | C. | m<2 | D. | m>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20}{27}$ | B. | $\frac{16}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{20}{27}$或$\frac{16}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
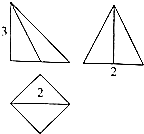
| A. | $\frac{13π}{4}$ | B. | $\frac{{\sqrt{13}π}}{2}$ | C. | 13π | D. | $\sqrt{13}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com