
分析 (Ⅰ)化简函数f(x),利用三角函数的有界性得出关于a的不等式,求不等式的解集即可;
(Ⅱ)根据f(-$\frac{π}{6}$)的值求出a,利用三角函数的图象与性质即可求出不等式的解集.
解答 解:(Ⅰ)函数f(x)=2acosx($\sqrt{3}$sinx+cosx)+a2
=2$\sqrt{3}$asinxcosx+2acos2x+a2
=a($\sqrt{3}$sin2x+1+cos2x)+a2
=2asin(2x+$\frac{π}{6}$)+a+a2,
∵-1≤sin(2x+$\frac{π}{6}$)≤1,a>0,
∴2asin(2x+$\frac{π}{6}$)+a+a2≤2a+a=a2+3a<4,
即a2+3a-4<0,
解得-4<a<1;
又a>0,所以a∈(0,1);
(Ⅱ)∵f(-$\frac{π}{6}$)=2asin[2×(-$\frac{π}{6}$)+$\frac{π}{6}$]+a+a2=a2=4,
且a>0,∴a=2,
∴f(x)=4sin(2x+$\frac{π}{6}$)+6;
当f(x)<8时,4sin(2x+$\frac{π}{6}$)+6<8,
即sin(2x+$\frac{π}{6}$)<$\frac{1}{2}$,
所以-$\frac{7π}{6}$+2kπ<2x+$\frac{π}{6}$<$\frac{π}{6}$+2kπ,k∈Z.
解得-$\frac{2π}{3}$+kπ<x<kπ,k∈Z,
所以不等式的解集为{ x|-$\frac{2π}{3}$+kπ<x<kπ,k∈Z}.
点评 本题考查了三角函数的化简与不等式的解法应用问题,也考查了三角函数的图象与性质的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
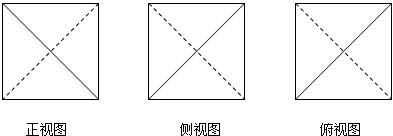
| A. | 3 | B. | 6 | C. | 3+$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com