
分析 (1)根据函数的奇偶性,求出m的值;(2)根据函数单调性的定义证明即可;(3)根据函数的奇偶性以及函数的单调性求出函数的最值即可.
解答 解:(1)若函数$f(x)=\frac{mx+1}{{1+{x^2}}}$是R上的偶函数,则f(-x)=f(x),
即$\frac{m(-x)+1}{{1+{{(-x)}^2}}}=\frac{mx+1}{{1+{x^2}}}$,对任意实数x恒成立,解得m=0.
(2)由(1)得:$f(x)=\frac{1}{{1+{x^2}}}$,
函数y=f(x)在(-∞,0]上为增函数,下证明:
设任意x1,x2∈(-∞,0]且x1<x2,即△x=x2-x1>0
则$△y=f({x_2})-f({x_1})=\frac{1}{1+x_2^2}-\frac{1}{1+x_1^2}$=$\frac{x_1^2-x_2^2}{(1+x_1^2)(1+x_2^2)}=\frac{{-({x_2}-{x_1})({x_2}+{x_1})}}{(1+x_1^2)(1+x_2^2)}$
∵x1,x2∈(-∞,0]且△x=x2-x1>0,
∴$\frac{{-({x_2}-{x_1})({x_2}+{x_1})}}{(1+x_1^2)(1+x_2^2)}>0$,即△y>0,
于是函数y=f(x)在(-∞,0]上为增函数.
(3)由(2)知,函数y=f(x)在(-∞,0]上为增函数,
又f(x)是偶函数,则y=f(x)在[0,+∞)上为减函数,
又$f(-3)=\frac{1}{10}$,f(0)=1,$f(2)=\frac{1}{5}$,
所以f(x)的最大值为1,最小值为$\frac{1}{10}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设a,b,c都是奇数 | B. | 假设a,b,c至少有两个是奇数 | ||
| C. | 假设a,b,c至多有一个是奇数 | D. | 假设a,b,c不都是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对嘉积中学的看法 | 非常好,嘉积中学奠定了 我一生成长的起点 | 很好,我的中学很快乐很充实 |
| A班人数比例 | $\frac{1}{2}$ | $\frac{1}{2}$ |
| B班人数比例 | $\frac{2}{3}$ | $\frac{1}{3}$ |
| C班人数比例 | $\frac{3}{4}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
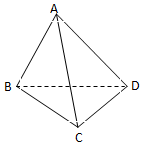 如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.
如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必经过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越大,模型的拟合效果越好 | |
| C. | 用R2来刻画回归效果,R2越大,说明模型的拟合效果越好 | |
| D. | 若散点图中的样本呈条状分布,则变量y和x之间具有线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
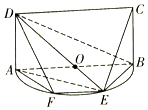 如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.
如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com