Question

11．在区间[0，1]上随机抽取两个数x，y，则事件“xy≥$\frac{1}{2}$”发生的概率为$\frac{1}{2}$-$\frac{1}{2}$ln2．

Answer 1

分析 设P（x，y），则P点落在边长为1的正方形OABC内部（含边界）．则满足条件xy$≥\frac{1}{2}$的点P落在曲线与正方形OABC所围成的区域内．使用定积分求出封闭区域的面积，则“xy≥$\frac{1}{2}$”发生的概率为$\frac{{S}_{阴影}}{{S}_{正方形ABCD}}$．

解答 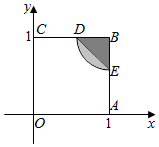解设P（x，y），∵0≤x，y≤1，
∴P点落在正方形OABC内部（含边界）．
作曲线y=$\frac{1}{2x}$，交正方形OABC于D，E两点，
则满足条件xy$≥\frac{1}{2}$的点P落在区域BDE内（含边界）．
由于S_阴影=$\frac{1}{2}×1$-${∫}_{\frac{1}{2}}^{1}\frac{1}{2x}dx$=$\frac{1}{2}-\frac{1}{2}ln2$．
∴“xy≥$\frac{1}{2}$”发生的概率为$\frac{{S}_{阴影}}{{S}_{正方形ABCD}}$=$\frac{1}{2}-\frac{1}{2}$ln2．
故答案为：$\frac{1}{2}-\frac{1}{2}ln2$．

点评 本题考查了几何概型的概率计算，作出符合条件的区域是解决几何概型的方法，属于中档题．