
分析 (1)代入递推式计算a2,a3,a4,根据计算结果猜想通项公式;
(2)根据特殊值比较大小,利用数学归纳法证明.
解答 解:(1)a2=$\frac{3×{1}^{2}-1+1+1}{2}$=2,
a3=$\frac{4×{2}^{2}-2×2+2+1}{5}$=3,
a4=$\frac{5×{3}^{2}-3×3+3+1}{10}$=4,
猜想:an=n.
证明:当n=1时,a1=1成立
假设n=k(k≥1)时,ak=k成立
则当n=k+1时,${a_{k+1}}=\frac{{(k+2)a_k^2-k{a_k}+k+1}}{{{a_k}^2+1}}=\frac{{(k+2){k^2}-k•k+k+1}}{{{k^2}+1}}=k+1$也成立
所以,${a_n}=n(n∈{N^*})$成立.
(2)猜想:当n≥4时,3${\;}^{{a}_{n}}$>(n-1)•2n+2n2,
下面用数学归纳法证明:
n=4时,左边=3${\;}^{{a}_{4}}$=34=81,右边=3•24+2•42=80,左边>右边,故结论成立;
假设当n=k(k≥4)时结论成立,即3k>(k-1)•2k+2k2,
两边同乘以3得:3k+1>3(k-1)•2k+6k2=k•2k+1+2(k+1)2+[(k-3)2k+4k2-4k-2],
∵k≥4时,(k-3)2k>0,4k2-4k-2=(2k-1)2-3≥46>0,
∴(k-3)2k+4k2-4k-2>0,
∴3k+1>k•2k+1+2(k+1)2,
即n=k+1时结论也成立.
∴当n≥4时,3n>(n-1)•2n+2n2成立.
点评 本题考查了数学归纳法的证明,掌握证明步骤,根据式子特点由n=k转化推导n=k+1是证明的关键.


科目:高中数学 来源: 题型:填空题
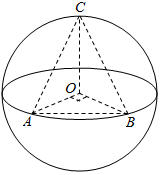 已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为$\frac{32}{3}$,则球O的表面积为64π.
已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为$\frac{32}{3}$,则球O的表面积为64π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程x3+ax-b=0没有实根 | B. | 方程x3+ax-b=0至多有一个实根 | ||
| C. | 方程x3+ax-b=0至多有两个实根 | D. | 方程x3+ax-b=0恰好有两个实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{32\sqrt{3}π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{64\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com