
分析 平面图形类比空间图形,二维类比三维得到类比平面几何的结论,证明时连接球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥,正四面体的体积,就是四个三棱锥的体积的和,求解即可.
解答 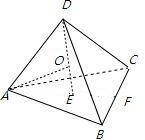 解:从平面图形类比空间图形,从二维类比三维,
解:从平面图形类比空间图形,从二维类比三维,
球心到正四面体一个面的距离即球的半径r,连接球心与正四面体的四个顶点.
把正四面体分成四个高为r的三棱锥,所以4×$\frac{1}{3}$S•r=$\frac{1}{3}$•S•h,r=$\frac{1}{4}$h.
(其中S为正四面体一个面的面积,h为正四面体的高)
所以它的内切球的半径r=$\frac{\sqrt{6}}{12}$a.
故答案为:$\frac{\sqrt{6}}{12}$a.
点评 本题主要考查类比推理.类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -$\frac{1}{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
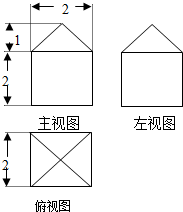
| A. | $(20+4\sqrt{3})c{m^2}$ | B. | $(20+4\sqrt{2})c{m^2}$ | C. | $(20+\sqrt{2})c{m^2}$ | D. | $(10+4\sqrt{2})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com