
【题目】如图,三棱锥![]() ,侧棱
,侧棱![]() ,底面三角形
,底面三角形![]() 为正三角形,边长为
为正三角形,边长为![]() ,顶点
,顶点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,有
,有![]() ,且
,且![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ⊥平面
⊥平面![]() ,如果存在,求
,如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.

【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:(1)证线面平行,则要在平面![]() 找一线与之平行即可,显然分析
找一线与之平行即可,显然分析![]() 即得证,(2)求二面角可借助空间直角坐标系将两个平面的法向量一一求出,再根据向量的数量积公式便可求解(3)存在问题可以根据结论反推即可,容易得因为
即得证,(2)求二面角可借助空间直角坐标系将两个平面的法向量一一求出,再根据向量的数量积公式便可求解(3)存在问题可以根据结论反推即可,容易得因为![]() ,所以
,所以![]() 与
与![]() 不垂直,故不存在
不垂直,故不存在
试题解析:
(Ⅰ)因为![]() ,且
,且![]() ,
, ![]() ,所以
,所以![]() ,
,
所以![]() .
.
因为![]() 为正三角形,所以
为正三角形,所以![]() ,
,
又由已知可知![]() 为平面四边形,所以
为平面四边形,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)由点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() 可得
可得![]() 平面
平面![]() ,
,
所以![]() ,
, ![]() .
.
以![]() 分别为
分别为![]() 建立空间直角坐标系,则由已知可知
建立空间直角坐标系,则由已知可知![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
平面![]() 的法向量
的法向量![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
由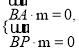 可得
可得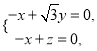
令![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量
的一个法向量![]() ,
,
所以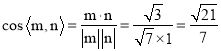 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)由(Ⅱ)可得![]() ,
, ![]() ,
,
因为![]() ,
,
所以![]() 与
与![]() 不垂直,
不垂直,
所以在线段![]() 上不存在点
上不存在点![]() 使得
使得![]() ⊥平面
⊥平面![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某单位附近只有甲、乙两个临时停车场,它们各有![]() 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的![]() ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
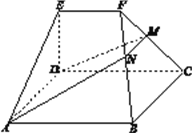
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 . 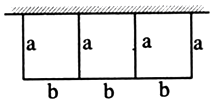
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的正方形,
的正方形, ![]() 底面
底面![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
(Ⅰ)求证: ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,试问在线段
,试问在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角 ![]() 的余弦值为
的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)抛物线的顶点在原点,坐标轴为对称轴,并经过点![]() ,求此抛物线的方程.
,求此抛物线的方程.
(Ⅱ)已知圆: ![]() (
(![]() ),把圆上的各点纵坐标不变,横坐标伸长到原来的
),把圆上的各点纵坐标不变,横坐标伸长到原来的![]() 倍得一椭圆.求椭圆方程,并证明椭圆离心率是与
倍得一椭圆.求椭圆方程,并证明椭圆离心率是与![]() 无关的常数.
无关的常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
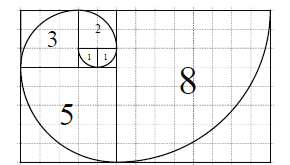
【题目】斐波那契数列![]() 满足:
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com