
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
���� ����ƽ������$\overrightarrow{a}$��$\overrightarrow{b}$�������������������ʿɵã���|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|��?$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$?$\overrightarrow{a}•\overrightarrow{b}$=0?��$\overrightarrow{a}$��$\overrightarrow{b}$���������жϳ����ۣ�
��� �⣺����ƽ������$\overrightarrow{a}$��$\overrightarrow{b}$����|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|��?$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$?$\overrightarrow{a}•\overrightarrow{b}$=0?��$\overrightarrow{a}$��$\overrightarrow{b}$����
�����ƽ������$\overrightarrow{a}$��$\overrightarrow{b}$����|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|���ǡ�$\overrightarrow{a}$��$\overrightarrow{b}$���ij�Ҫ������
��ѡ��C��
���� ���⿼���������������������ʡ����������ж�������������ֱ���������Ĺ�ϵ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
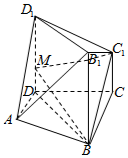 ��ͼ��������ABCD-B1C1D1�У�������BB1D1D��ƽ��ABCD��D1D��CC1��ƽ��D1DCC1��ƽ��B1BCC1���ɵĶ���ǵ�����ֵΪ$\frac{2}{3}$��BC=3��CD=2CC1=2��AD=$\sqrt{5}$��AD��BC��MΪDD1������һ�㣮
��ͼ��������ABCD-B1C1D1�У�������BB1D1D��ƽ��ABCD��D1D��CC1��ƽ��D1DCC1��ƽ��B1BCC1���ɵĶ���ǵ�����ֵΪ$\frac{2}{3}$��BC=3��CD=2CC1=2��AD=$\sqrt{5}$��AD��BC��MΪDD1������һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��2�� | B�� | ∅ | C�� | ��-�ޣ�-1���ȣ�1��+�ޣ� | D�� | ��-1��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 62 | C�� | -57 | D�� | -56 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com