
分析 (1)解不等式求出M,N,结合题意计算即可;
(2)解不等式求出集合H,结合(1)中N△M,分类讨论,可得(N△M)△H.
解答 解:(1)M={x|1<x<3},N={x|x2-6x+8≤0}={x|2≤x≤4};
根据题意,U=R,∁UN={x|x<2或x>4},
∴M△N=M∩(∁UN)={x|1<x<2},
又∁UM={x|x≤1或x≥3},
∴N△M=N∩(∁UM)={x|3≤x≤4};
(2)∵H={x||x-a|≤2}=[a-2,a+2],
∴(N△M)△H=(N△M)∩(CUH)=(1,2)∩[(-∞,a-2)∪(a+2,+∞)],
当a-2≥2,或a+2≤1,即a≥4,或a≤-1时,(N△M)△H=(1,2);
当1<a-2<2,即3<a<4时,(N△M)△H=(1,a-2);
当1<a+2<2,即-1<a<0时,(N△M)△H=(a+2,2);
当a-2≤1,且a+2≥2,即0≤a≤3时,(N△M)△H=∅.
点评 本题考查了集合的交集,并集,补集的定义与运算问题,是综合性题目.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|2≤x≤3} | B. | {x|-2≤x≤3} | C. | {x|-2≤x<2} | D. | {x|-4<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
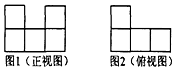 用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )
用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )| A. | 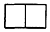 | B. | 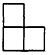 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com