练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．设f°（x）=cosx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn（x）=f′n-1（x）（n∈N*），则f2011（x）=（　　）
    A．cosxB．-sinxC．-cosxD．sinx

    分析 由已知，f0（x）=cosx，f1（x）=f0′（x）=-sinx，f2（x）=f1′（x）=-cosx，f3（x）=f2′（x）=sinx，f4（x）=f3′（x）=cosx，发现fn（x）以4为周期，结果循环出现，利用此规律将n=2011转化为n=3的情况求解．

    解答 解：∵f0（x）=cosx，
    ∴f1（x）=f0′（x）=-sinx，
    f2（x）=f1′（x）=-cosx，
    f3（x）=f2′（x）=sinx，
    f4（x）=f3′（x）=cosx
    …
    从第五项开始，fn（x）的解析式重复出现，每4次一循环．
    ∴f2011（x）=f4×502+3（x）=f3（x）=sinx，
    故选：D．

    点评 本题考查函数求导运算，由于f2011（x）中下标数值2011较大，所以探究fn（x）的周期性成为必要与自然，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

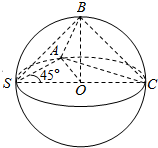    1．已知球的直径SC=4，A，B是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为（　　）
    A．$\frac{2\sqrt{3}}{3}$B．$\frac{\sqrt{3}}{3}$C．$\frac{5\sqrt{3}}{3}$D．$\frac{4\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知${（\sqrt{x}+\frac{1}{{\root{4}{x}}}）^n}$展开式中各项的二项式系数和为64．
    （1）求n的值；
    （2）求展开式中的常数项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知加工某一零件共需两道工序，第1，2道工序的不合格品率分别为2%和5%，且各道工序互不影响，则加工出来的零件是不合格品的概率为0.069．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若复数$z=\frac{1+i}{1-i}，则{z^{2010}}$=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．与直线x-y+4=0和圆x2+y2-2x+2y=0都相切的半径最小的圆的方程是（　　）
    A．（x+1）2+（y+1）2=2B．（x+1）2+（y-1）2=2C．（x+1）2+（y+1）2=4D．（x+1）2+（y-1）2=4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=x3-3x2+3x-2．
    （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
    （2）当x∈[-2，2]时，求f（x）的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知b＞a＞0，求b2+$\frac{1}{a（b-a）}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．化简$\overrightarrow{BC}$+$\overrightarrow{AB}$-$\overrightarrow{AC}$的结果是（　　）
    A．$\overrightarrow{0}$B．2$\overrightarrow{BC}$C．-2$\overrightarrow{BC}$D．2$\overrightarrow{AC}$

    查看答案和解析>>

    同步练习册答案