
分析 (1)利用函数的最小值列出方程解得ω,利用平行变换可得解函数g(x)的解析式.
(2)由题意可得函数的零点,可解得A,由余弦定理可得25≥bc,利用三角形的面积公式即可得解.
解答 解:(1)∵函数f(x)=2sinωx(0<ω<3)在[-$\frac{π}{6}$,0]上的最小值为-$\sqrt{3}$,
∴2sin(-$\frac{π}{6}$ω)=-$\sqrt{3}$,解得ω=2,
把f(x)的图象上所有的点向右平移$\frac{π}{3}$个单位后,
得到的函数g(x)=2sin[2(x-$\frac{π}{3}$)]=2sin(2x-$\frac{2π}{3}$),
∴函数g(x)的解析式为:g(x)=2sin(2x-$\frac{2π}{3}$).
(2)∵函数g(x)在y轴右侧的第一个零点恰为A,
∴由2sin(2x-$\frac{2π}{3}$)=0,解得2x-$\frac{2π}{3}$=kπ,k∈Z,可得:A=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,
令k=0,可得A=$\frac{π}{3}$.
∵a=5,
∴由余弦定理可得:25=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
∴S△ABC=$\frac{1}{2}$bcsinA≤$\frac{1}{2}$×25×$\frac{\sqrt{3}}{2}$=$\frac{25\sqrt{3}}{4}$.
故△ABC的面积S的最大值为:$\frac{25\sqrt{3}}{4}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,余弦定理,三角形面积公式的应用,属于基本知识的考查.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
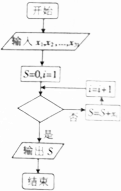 用xi表示某人2016年3月份第i天的手机流量,计算该人3月的手机流量总量的程序框图如图,则判断框中可以填入( )
用xi表示某人2016年3月份第i天的手机流量,计算该人3月的手机流量总量的程序框图如图,则判断框中可以填入( )| A. | i≤31? | B. | i<31? | C. | i>31? | D. | i≥31? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在某个位置,使得直线AB和直线CD垂直 | |
| B. | 存在某个位置,使得直线AC和直线BD垂直 | |
| C. | 存在某个位置,使得直线AD和直线BC垂直 | |
| D. | 无论翻折到什么位置,以上三组直线均不垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com