
���� ��1���������Ĵ�������������������������¼�����n=${C}_{10}^{3}$=120�����ټ�1�����ٵ���60km/h�Ķ����¼���û�м����ٵ���60km/h�ij������ɴ����ö����¼����ʼ��㹫ʽ��������ټ�1�����ٵ���60km/h�ĸ��ʣ�
��2������֪�������ļ��ס��ҵĸ��ʶ���$\frac{3}{5}$���������ļ����ĸ�����$\frac{1}{5}$������֪��X�Ŀ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��� �⣺��1����ijʱ����������6���ٶȳ���100km/h��4���ٶȵ���60km/h������������ʻ��
�������Ĵ��������������������¼�����n=${C}_{10}^{3}$=120��
���ټ�1�����ٵ���60km/h�Ķ����¼���û�м����ٵ���60km/h�ij�����
�����ټ�1�����ٵ���60km/h�ĸ��ʣ�
p=1-$\frac{{C}_{6}^{3}}{{C}_{10}^{3}}$=$\frac{5}{6}$��
��2������֪�������ļ��ס��ҵĸ��ʶ���$\frac{3}{5}$���������ļ����ĸ�����$\frac{1}{5}$��
����֪��X�Ŀ���ȡֵΪ0��1��2��3��
P��X=0��=��1-$\frac{3}{5}$����1-$\frac{3}{5}$����1-$\frac{1}{5}$��=$\frac{16}{125}$��
P��X=1��=${C}_{2}^{1}��\frac{3}{5}����1-\frac{3}{5}��•��1-\frac{1}{5}��$+${C}_{2}^{0}��1-\frac{3}{5}��^{2}��\frac{1}{5}$=$\frac{52}{125}$��
P��X=2��=${C}_{2}^{2}��\frac{3}{5}��^{2}•��1-\frac{1}{5}��$+${C}_{2}^{1}��\frac{3}{5}����1-\frac{3}{5}��•\frac{1}{5}$=$\frac{48}{125}$��
P��X=3��=$\frac{3}{5}��\frac{3}{5}��\frac{1}{5}$=$\frac{9}{125}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{16}{125}$ | $\frac{52}{125}$ | $\frac{48}{125}$ | $\frac{9}{125}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ�����ֲ���Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
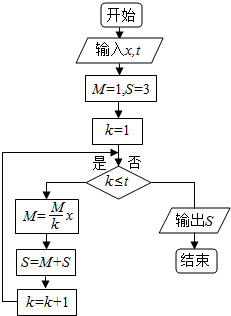
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
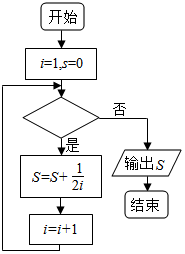
| A�� | i��1007 | B�� | i��1008 | C�� | i��1008 | D�� | i��1007 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
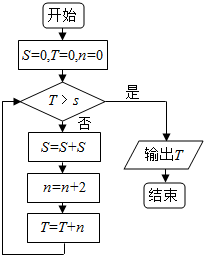
| A�� | 32 | B�� | 30 | C�� | 20 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com