
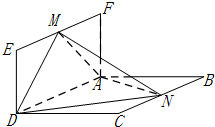
 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF,∠CBA=60°.
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF,∠CBA=60°.分析 (1)证明AN⊥DM,DM⊥AM,利用线面垂直的判定定理证明:DM⊥平面MNA;
(2)利用等体积,求出点M到平面ADN的距离,作AH⊥MN交MN于点H,AH为求点A到平面DMN的距离,利用等面积求点A到平面DMN的距离.
解答 证明:(1)连接AC,在菱形ABCD中,
∵∠CBA=60°且AB=AC,
∴△ABC为等边三角形.
∵N是BC的中点,
∴AN⊥BC,AN⊥BC.
∵ABCD⊥平面ADEF,AN?平面ADEF,ABCD∩平面ADEF=AD,
∴AN⊥平面ABEF.
∵DM?平面ADEF,
∴AN⊥DM.
∵矩形ADEF中,AD=2AF,M是的中点,
∴△AMF为等腰直角三角形,
∴∠AMF=45°,
同理可证∠DME=45°,
∴∠DAM=90°,
∴DM⊥AM.
∵AM∩AN=N,AM?平面MNA,AN?平面MNA,
∴DM⊥平面MNA.
解:(2)设AF=x,则AB=2AF=2x,
在Rt△ABN中,AB=2x,BN=x,∠ABN=60°,
∴$AN=\sqrt{3}x$.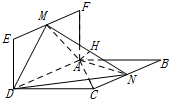
∴${S_{△ADN}}=\frac{1}{2}•2x•\sqrt{3}x=\sqrt{3}{x^2}$.
∵ABCD⊥平面ADEF,FA⊥AD,ABCD∩平面ADEF=AD,
∴FA⊥平面ABCD.
设h为点M到平面ADN的距离,则h=FA=x.
∴${V_{M-ADN}}=\frac{1}{3}{V_{△CDF}}•h=\frac{1}{3}•\sqrt{3}{x^2}•x=\frac{{\sqrt{3}}}{3}{x^3}$,
∵${V_{M-ADN}}={V_{D-AMN}}=\frac{{\sqrt{3}}}{3}$,
∴x=1.
作AH⊥MN交MN于点H.
∵DM⊥平面MNA,
∴DM⊥AH.
∴AH⊥平面DMN,
即AH为求点A到平面DMN的距离,
∵在Rt△MNA中,$MA=\sqrt{2}$,$AN=\sqrt{3}$,
∴$AH=\frac{{\sqrt{30}}}{5}$.
∴点A到平面DMN的距离为$\frac{{\sqrt{30}}}{5}$.
点评 本题主要考查了直线与平面垂直的判定与性质,以及着重考查了棱锥的体积公式,考查空间想象能力、运算能力.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
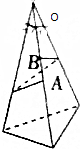 如图,在以O为顶点的三棱锥中,过O的三条棱两两相交都是30°,在一条棱上取A、B两点,OA=4cm,OB=3cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.
如图,在以O为顶点的三棱锥中,过O的三条棱两两相交都是30°,在一条棱上取A、B两点,OA=4cm,OB=3cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正三棱柱ABC-A1B1C1,各棱长都是2,M是AC中点.
如图,正三棱柱ABC-A1B1C1,各棱长都是2,M是AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,PA=AB=AD=2,BC=4,M是PD的中点.
如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,PA=AB=AD=2,BC=4,M是PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com