
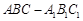 中,
中,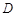 、
、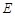 分别是棱
分别是棱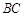 、
、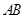 的中点,点
的中点,点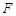 在棱
在棱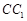 上,已知
上,已知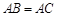 ,
,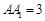 ,
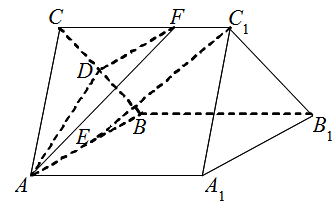
,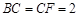 .
.
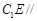 平面
平面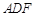 ;
;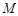 在棱
在棱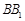 上,当
上,当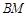 为何值时,平面
为何值时,平面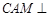 平面
平面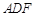 ?
?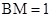
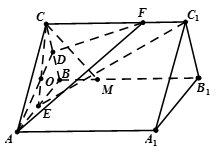
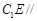 平面
平面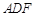 ,只需在平面内找一条直线与
,只需在平面内找一条直线与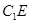 平行,如果不容易直接找到,可以将
平行,如果不容易直接找到,可以将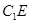 平移到平面内,平移直线的方法一般有①中位线平移;②平行四边形对边平行平移;③成比例线段平移,该题连接
平移到平面内,平移直线的方法一般有①中位线平移;②平行四边形对边平行平移;③成比例线段平移,该题连接 交
交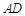 于
于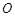 ,连接
,连接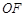 ,可证
,可证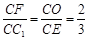 ,从而
,从而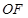 ∥
∥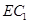 ,进而可证
,进而可证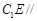 平面
平面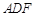 ;(2)该题主要是如何分析得到
;(2)该题主要是如何分析得到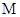 的位置,然后再证明,由已知可得平面
的位置,然后再证明,由已知可得平面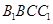
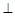 平面
平面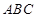 ,进而可证
,进而可证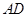
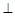 平面
平面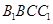 ,故AD
,故AD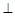 CM,只需有
CM,只需有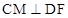 ,则CM
,则CM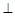 平面
平面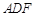 ,从而平面
,从而平面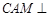 平面
平面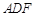 ,那么如何保证
,那么如何保证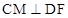 呢?在矩形
呢?在矩形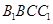 中,只需
中,只需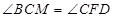 ,则
,则
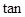
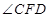 ,则
,则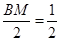 ,所以
,所以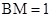 ,倒过来,再证明平面
,倒过来,再证明平面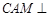 平面
平面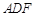 即可.
即可. 交
交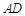 于
于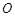 ,连接
,连接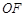 ,因为CE,AD为△ABC中线,所以O为△ABC的重心,
,因为CE,AD为△ABC中线,所以O为△ABC的重心,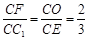 ,从而OF//C1E,OF
,从而OF//C1E,OF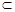 面ADF,
面ADF,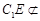 平面
平面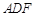 ,所以
,所以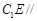 平面
平面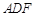 ;
;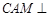 平面
平面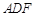 .
.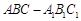 中,由于
中,由于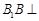 平面ABC,BB1
平面ABC,BB1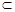 平面B1BCC1,所以平面B1BCC1
平面B1BCC1,所以平面B1BCC1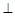 平面ABC,由于AB=AC,
平面ABC,由于AB=AC,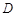 是
是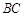 中点,所以
中点,所以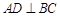 ,又平面B1BCC1∩平面ABC=BC,所以AD
,又平面B1BCC1∩平面ABC=BC,所以AD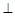 平面B1BCC1, 而CM
平面B1BCC1, 而CM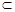 平面B1BCC1,于是AD
平面B1BCC1,于是AD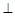 CM,因为BM =CD=1,BC= CF=2,所以
CM,因为BM =CD=1,BC= CF=2,所以 ≌
≌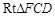 ,所CM
,所CM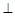 DF,
DF,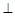 平面
平面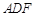 ,CM
,CM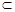 平面CAM,所以平面
平面CAM,所以平面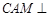 平面
平面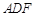 ,∴当BM=1时,平面
,∴当BM=1时,平面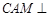 平面
平面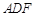 .
.

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
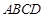 是菱形,
是菱形,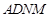 是矩形,平面
是矩形,平面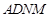 ⊥平面
⊥平面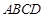 ,
,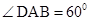 ,
,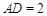 ,
,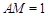 ,
,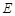 是
是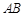 的中点.
的中点.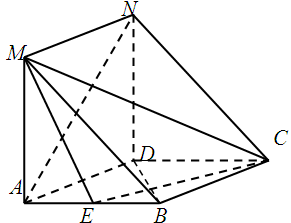
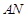 //平面
//平面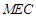 ;
;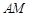 上是否存在点
上是否存在点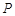 ,使二面角
,使二面角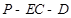 的大小为
的大小为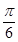 ?若存在,求出
?若存在,求出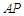 的长
的长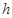 ;若不存在,请说明理由.
;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
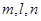 和平面
和平面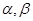 的四个命题:
的四个命题: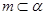 ,
,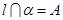 ,点
,点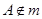 ,则
,则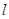 与
与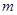 不共面;
不共面;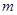 、
、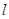 是异面直线,
是异面直线,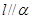 ,
,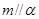 ,且
,且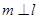 ,
,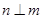 ,则
,则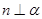 ;
;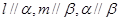 ,则
,则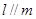 ;
;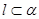 ,
,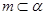 ,
,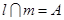 ,
,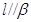 ,
,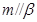 ,则
,则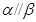 .
.| A.① | B.② | C.④ | D.③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.底面是正方形,有两个侧面是矩形 |
| B.每个侧面都是全等矩形的四棱柱 |
| C.底面是菱形,且有一个顶点处的三条棱两两垂直 |
| D.底面是正方形,有两个相邻侧面垂直于底面 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
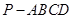 中,点
中,点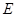 为
为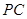 中点,则下列命题正确的是( )
中点,则下列命题正确的是( )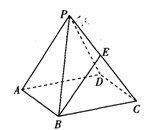
A.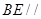 面 面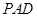 ,且直线 ,且直线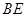 到面 到面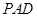 距离为 距离为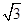 |
B.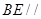 面 面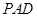 ,且直线 ,且直线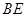 到面 到面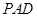 距离为 距离为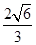 |
C.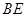 不平行于面 不平行于面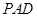 ,且 ,且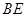 与平面 与平面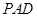 所成角大于 所成角大于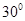 |
D.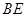 不平行于面 不平行于面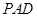 ,且 ,且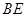 与平面 与平面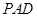 所成角小于 所成角小于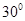 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com