
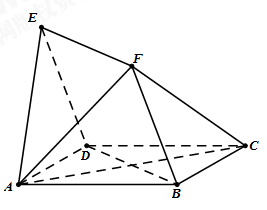
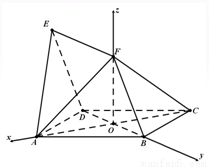
(本小题共14分)如图,四边形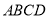 与
与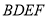 均为菱形,
均为菱形, 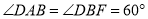 ,且
,且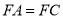 .
.
(Ⅰ)求证: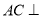 平面
平面 ;
;
(Ⅱ)求证: ∥平面
∥平面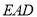 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)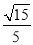
【解析】
试题分析:(Ⅰ)证明:设AC与BD相交于点O,连结FO.
因为 四边形ABCD为菱形,所以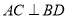 ,
,
且O为AC中点. 1分
又FA=FC,所以 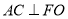 . 3分
. 3分
因为 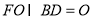 ,
,
所以 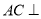 平面BDEF. 4分
平面BDEF. 4分
(Ⅱ)证明:因为四边形ABCD与BDEF均为菱形,
所以AD//BC,DE//BF,
所以 平面FBC//平面EAD. 7分
又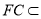 平面FBC,
平面FBC,
所以FC// 平面EAD. 8分
(Ⅲ)【解析】
因为四边形BDEF为菱形,且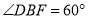 ,所以△DBF为等边三角形.
,所以△DBF为等边三角形.
因为O为BD中点,所以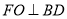 ,故
,故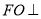 平面ABCD.
平面ABCD.
由OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O-xyz. 9分
设AB=2.因为四边形ABCD为菱形, ,则BD=2,所以OB=1,
,则BD=2,所以OB=1,
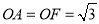 .
.
所以 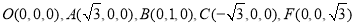 .
.
所以 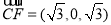 ,
,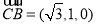 .
.
设平面BFC的法向量为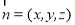 ,则有
,则有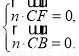
所以  取x=1,得
取x=1,得 . 12分
. 12分
易知平面AFC的法向量为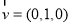 . 13分
. 13分
由二面角A-FC-B是锐角,得  .
.
所以二面角A-FC-B的余弦值为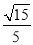 . 14分
. 14分
考点:本题考查线面平行的判定,线面垂直的判定,求二面角


科目:高中数学 来源:2014-2015学年湖南省株洲市高三教学质量统一检测一文科数学试卷(解析版) 题型:选择题
在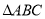 中,若角
中,若角 所对的三边
所对的三边 成等差数列,给出下列结论:
成等差数列,给出下列结论:
①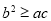 ;②
;②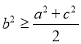 ;③
;③ ;④
;④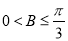 .
.
其中正确的结论是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省株洲市高三教学质量统一检测一文科数学试卷(解析版) 题型:选择题
设数列{an}是等比数列,函数y=x2-x-2的两个零点是 ,则
,则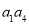 =( )
=( )
A.2 B.1 C.-1 D.-2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三上学期期末考试文科数学试卷(解析版) 题型:填空题
为了解某厂职工家庭人均月收入情况,调查了该厂80户居民月收入,列出频率分布表
如下:
按家庭人均月收入分组(百元) | 第一组
| 第二组
| 第三组
| 第四组
| 第五组
| 第六组
|
频率 | 0.1 | 0.2 | 0.15 |
| 0.1 | 0.1 |
则这80户居民中, 家庭人均月收入在 元之间的有 户(用数字作答);假设家庭人均月收入在第一组和第二组的为中低收入家庭,现从该厂全体职工家庭中随机抽取一个家庭,估计该家庭为中低收入家庭的概率是 .
元之间的有 户(用数字作答);假设家庭人均月收入在第一组和第二组的为中低收入家庭,现从该厂全体职工家庭中随机抽取一个家庭,估计该家庭为中低收入家庭的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com