
 已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线C上的点,且|$\overrightarrow{DF}$|=3.
已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线C上的点,且|$\overrightarrow{DF}$|=3.分析 (1)利用抛物线的定义,求出p,即可求出求抛物线C的方程;设直线l的方程为x=my+1-2m,代入y2=8x,利用AE=4EB,求出m,即可求直线l的方程;
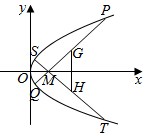
(2)设出PQ:x=ky+m,与抛物线方程联立,求出G的坐标,同理可得H的坐标,求出GH的斜率,可得GH的方程,从而可得直线GH过定点,表示出△MGH面积,利用基本不等式,即可求出△MGH面积S的最小值.
解答 解:(1)∵点F是抛物线y2=2px(p>0)的焦点,点D(1,y0)是抛物线C上的点,且|$\overrightarrow{DF}$|=3,
∴1+$\frac{p}{2}$=3,
解得:p=4,∴y2=8x.
设直线l的方程为x=my+1-2m,A(x1,y1),B(x2,y2),
x=my+1-2m代入y2=8x,可得y2-8my-8+16m=0,
∴y1+y2=8m①,y1y2=-8+16m②,
∵AE=4EB,
∴(1-x1,2-y1)=4(x2-1,y2-2),
∴2-y1=4(y2-2)③,
由①②③可得m=$\frac{7}{8}$或$\frac{1}{8}$,
∴直线l的方程为8x-7y+6=0或8x-y-6=0;
(2)显然PQ,ST的斜率都存在且不为零.
设PQ:x=ky+m,P(x1,y1),Q(x2,y2),
代入y2=8x,得,y2-8ky-8m=0,
∴yG=4k,xG=4k2+m.
同理yH=-$\frac{4}{k}$,xH=$\frac{4}{{k}^{2}}$+m.
即G(4k2+m,4k),H($\frac{4}{{k}^{2}}$+m,-$\frac{4}{k}$),
∴kGH=$\frac{k}{{k}^{2}-1}$.
∴GH:y-4k=($\frac{k}{{k}^{2}-1}$)(x-4k2-m)
∴直线GH过定点(4+m,0).
∴S=$\frac{1}{2}$×|4+m-m|×|4k+$\frac{4}{k}$|≥16,
当|4k|=|$\frac{4}{k}$|,即k=±1时,Smin=16.
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查三角形面积的计算,考查基本不等式的运用,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
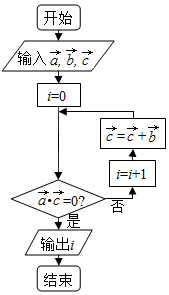 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{1}{4}$ | m | $\frac{1}{3}$ |
| A. | $\frac{7}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com