
| A. | sinx+cosx | B. | $y=\sqrt{1-{2^x}}$ | C. | y=2x2+x+1 | D. | $y={2^{-\frac{x}{2}}}$ |
科目:高中数学 来源: 题型:填空题
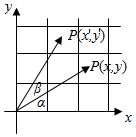 如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -3 | C. | -1 | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知定义在R上的函数f(x)及其导函数f′(x)的图象如图所示,则函数y=e-xf(x)的减区间为( )
已知定义在R上的函数f(x)及其导函数f′(x)的图象如图所示,则函数y=e-xf(x)的减区间为( )| A. | (0,1),(4,+∞) | B. | (-∞,1) | C. | (1,+∞) | D. | (-∞,0),(1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 第一组 | 第二组 | 第二组 | 第四组 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 6 | 4 | 22 | 20 |
| 频率 | 0.06 | 0.04 | 0.22 | 0.20 |
| 组号 | 第五组 | 第六组 | 第七组 | 第八组 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 18 | a | 10 | 5 |
| 频率 | b | 0.15 | 0.10 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {1,3} | C. | {2,6} | D. | {1,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{π}{2}]$ | B. | [0,π] | C. | $[\frac{π}{2},π]$ | D. | $[\frac{π}{2},\frac{3π}{2}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com