
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | 3 |
分析 $\frac{y}{x}$可看作点(x,y)与原点连线的斜率,所以问题转化为求圆上一点与原点连线中斜率最大值的问题.
解答 解:圆的圆心坐标(2,0)半径为$\sqrt{3}$,如图: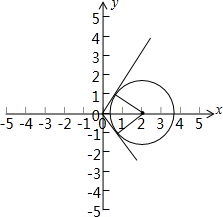
设$\frac{y}{x}$=k,则y=kx,
所以k为过原点与圆x2+y2-4x+1=0上的点连线的斜率.
由几何意义知,直线与圆相切时,直线的斜率取得最大值或最小值,
圆的半径为$\sqrt{3}$,圆心到原点的距离为2,
所以k=tan60°=$\sqrt{3}$,
所以$\frac{y}{x}$的最大值是$\sqrt{3}$.
故选:A.
点评 考查$\frac{y}{x}$的几何意义,类似于本题中这样的分式形式求最值时一般都转化为求直线的斜率来解决.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -1003 | D. | 1003 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 10 | C. | 25 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{125}{12}$π | B. | $\frac{125}{9}$π | C. | $\frac{125}{6}$π | D. | $\frac{125}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
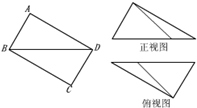 如图,在矩形ABCD中,$AB=\frac{3}{2}$,BC=2,沿BD将矩形ABCD折叠,连结AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的体积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2}$,BC=2,沿BD将矩形ABCD折叠,连结AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的体积为( )| A. | $\frac{6}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com