
 ��
��| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� ���ݵ�E��ƽ��ABC1D1�ľ�����ڵ�1��ƽ��ABC1D1�ľ��룬�жϢټ��ɣ�
ֱ��BC��ƽ��ABC1D1���ƽ�Ϊ��CB1C1������Rt��CB1C1��⼴�ɣ�
�ѿռ��ı���ABCD1�ڸ����������ң�ǰ�����µ���Ӱ�������ж���Сֵ���ɣ�
����ƽ�У��ཻ�ó���������������У���AB��CC1����������5����������BB1��D1C1��DC��AA1��BC��
��� �⣺��EB1��ƽ��ABC1D1��
���E��ƽ��ABC1D1�ľ�����ڵ�B1��ƽ��ABC1D1�ľ��룬
���E��ƽ��ABC1D1�ľ���Ϊ$\frac{\sqrt{2}}{2}$��
�ʢٲ���ȷ��
��ֱ��BC��ƽ��ABC1D1���ƽ�Ϊ��CB1C1��
����Rt��CB1C1�У���CB1C1=45�㣬
�ʢ���ȷ��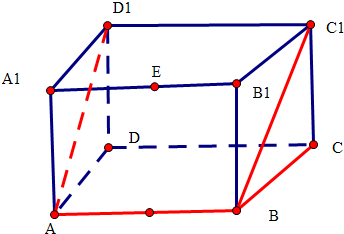
�߿ռ��ı���ABCD1�ڸ����������������Ӱ���Ϊ1��
�ռ��ı���ABCD1�ڸ����������ң�ǰ�����Ӱ���Ϊ$\frac{1}{2}$��
��ռ��ı���ABCD1�ڸ�����������������Ӱ�������СֵΪ$\frac{1}{2}$��
�ʢ���ȷ��
�������������������AB��CC1����������5����������BB1��D1C1��DC��AA1��BC��
�����ȷ��
��ѡ��C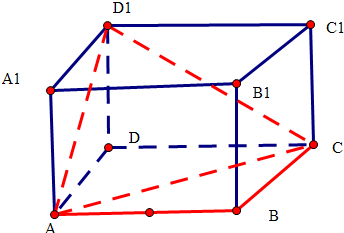
���� �����ۺϲο���������ļ������ʣ��ռ�ֱ�ߣ�ƽ��ľ��룬�н����⣬������Ϊƽ����⣬�����е��⣬�ؼ�����ϸ��ͼ�ó��������߶Σ��нǣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ������ABCD-A1B1C1D1���ⳤΪ2���߶�B1D1������������E��F��EF=$\sqrt{2}$�����������������
��ͼ��ʾ������ABCD-A1B1C1D1���ⳤΪ2���߶�B1D1������������E��F��EF=$\sqrt{2}$������������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͳ��ijУѧ������ѧ·������ʱ��������120���ӣ���У�����ȡ��������У��ѧ��������ѧ·������ʱ�䣨��λ�����ӣ����е��飬�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ��
��ͳ��ijУѧ������ѧ·������ʱ��������120���ӣ���У�����ȡ��������У��ѧ��������ѧ·������ʱ�䣨��λ�����ӣ����е��飬�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com