
【题目】已知函数f(x)=(x﹣2)ex+a(x﹣1)2有两个零点.
(1)求a的取值范围;
(2)设x1 , x2是f(x)的两个零点,证明:x1+x2<2.
【答案】
(1)
解:∵函数f(x)=(x﹣2)ex+a(x﹣1)2,
∴f′(x)=(x﹣1)ex+2a(x﹣1)=(x﹣1)(ex+2a),
①若a=0,那么f(x)=0(x﹣2)ex=0x=2,
函数f(x)只有唯一的零点2,不合题意;
②若a>0,那么ex+2a>0恒成立,
当x<1时,f′(x)<0,此时函数为减函数;
当x>1时,f′(x)>0,此时函数为增函数;
此时当x=1时,函数f(x)取极小值﹣e,
由f(2)=a>0,可得:函数f(x)在x>1存在一个零点;
当x<1时,ex<e,x﹣2<﹣1<0,
∴f(x)=(x﹣2)ex+a(x﹣1)2>(x﹣2)e+a(x﹣1)2=a(x﹣1)2+e(x﹣1)﹣e,
令a(x﹣1)2+e(x﹣1)﹣e=0的两根为t1,t2,且t1<t2,
则当x<t1,或x>t2时,f(x)>a(x﹣1)2+e(x﹣1)﹣e>0,
故函数f(x)在x<1存在一个零点;
即函数f(x)在R是存在两个零点,满足题意;
③若﹣ ![]() <a<0,则ln(﹣2a)<lne=1,
<a<0,则ln(﹣2a)<lne=1,
当x<ln(﹣2a)时,x﹣1<ln(﹣2a)﹣1<lne﹣1=0,
ex+2a<eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)>0恒成立,故f(x)单调递增,
当ln(﹣2a)<x<1时,x﹣1<0,ex+2a>eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)<0恒成立,故f(x)单调递减,
当x>1时,x﹣1>0,ex+2a>eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)>0恒成立,故f(x)单调递增,
故当x=ln(﹣2a)时,函数取极大值,
由f(ln(﹣2a))=[ln(﹣2a)﹣2](﹣2a)+a[ln(﹣2a)﹣1]2=a{[ln(﹣2a)﹣1]2+1}<0得:
函数f(x)在R上至多存在一个零点,不合题意;
④若a=﹣ ![]() ,则ln(﹣2a)=1,
,则ln(﹣2a)=1,
当x<1=ln(﹣2a)时,x﹣1<0,ex+2a<eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)>0恒成立,故f(x)单调递增,
当x>1时,x﹣1>0,ex+2a>eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)>0恒成立,故f(x)单调递增,
故函数f(x)在R上单调递增,
函数f(x)在R上至多存在一个零点,不合题意;
⑤若a<﹣ ![]() ,则ln(﹣2a)>lne=1,
,则ln(﹣2a)>lne=1,
当x<1时,x﹣1<0,ex+2a<eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)>0恒成立,故f(x)单调递增,
当1<x<ln(﹣2a)时,x﹣1>0,ex+2a<eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)<0恒成立,故f(x)单调递减,
当x>ln(﹣2a)时,x﹣1>0,ex+2a>eln(﹣2a)+2a=0,
即f′(x)=(x﹣1)(ex+2a)>0恒成立,故f(x)单调递增,
故当x=1时,函数取极大值,
由f(1)=﹣e<0得:
函数f(x)在R上至多存在一个零点,不合题意;
综上所述,a的取值范围为(0,+∞)
(2)
证明:∵x1,x2是f(x)的两个零点,
∴f(x1)=f(x2)=0,且x1≠1,且x2≠1,
∴﹣a= ![]() =
= ![]() ,
,
令g(x)= ![]() ,则g(x1)=g(x2)=﹣a,
,则g(x1)=g(x2)=﹣a,
∵g′(x)= ![]() ,
,
∴当x<1时,g′(x)<0,g(x)单调递减;
当x>1时,g′(x)>0,g(x)单调递增;
设m>0,则g(1+m)﹣g(1﹣m)= ![]() =
= ![]() ,
,
设h(m)= ![]() ,m>0,
,m>0,
则h′(m)= ![]() >0恒成立,
>0恒成立,
即h(m)在(0,+∞)上为增函数,
h(m)>h(0)=0恒成立,
即g(1+m)>g(1﹣m)恒成立,
令m=1﹣x1>0,
则g(1+1﹣x1)>g(1﹣1+x1)g(2﹣x1)>g(x1)=g(x2)2﹣x1>x2,
即x1+x2<2.
【解析】利用导数研究函数的极值;函数的零点.(1)由函数f(x)=(x﹣2)ex+a(x﹣1)2可得:f′(x)=(x﹣1)ex+2a(x﹣1)=(x﹣1)(ex+2a),对a进行分类讨论,综合讨论结果,可得答案.(2)设x1 , x2是f(x)的两个零点,则﹣a= ![]() =
= ![]() ,令g(x)=
,令g(x)= ![]() ,则g(x1)=g(x2)=﹣a,分析g(x)的单调性,令m>0,则g(1+m)﹣g(1﹣m)=
,则g(x1)=g(x2)=﹣a,分析g(x)的单调性,令m>0,则g(1+m)﹣g(1﹣m)= ![]() ,
,
设h(m)= ![]() ,m>0,利用导数法可得h(m)>h(0)=0恒成立,即g(1+m)>g(1﹣m)恒成立,令m=1﹣x1>0,可得结论.本题考查的知识点是利用导数研究函数的极值,函数的零点,分类讨论思想,难度较大.
,m>0,利用导数法可得h(m)>h(0)=0恒成立,即g(1+m)>g(1﹣m)恒成立,令m=1﹣x1>0,可得结论.本题考查的知识点是利用导数研究函数的极值,函数的零点,分类讨论思想,难度较大.
【考点精析】通过灵活运用函数的极值与导数和函数的零点,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点即可以解答此题.
是极小值;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点即可以解答此题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系内从点P1(0,0)作x轴的垂线交曲线y=ex于点Q1(0,1),曲线在Q1点处的切线与x轴交于点P2.再从P2作x轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,Q1;P2,Q2;…;Pn,Qn,记![]() 点的坐标为(
点的坐标为(![]() ,0)(k=1,2,…,n).
,0)(k=1,2,…,n).

(1)试求![]() 与
与![]() 的关系(k=2,…,n);
的关系(k=2,…,n);
(2)求|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E与二面角C﹣BE﹣F都是60°.
(1)证明平面ABEF⊥平面EFDC;
(2)求二面角E﹣BC﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)≥0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线![]() ,已知过点
,已知过点![]() 的直线的参数方程为:
的直线的参数方程为: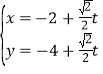 (t为参数),直线与曲线C分别交于M,N.
(t为参数),直线与曲线C分别交于M,N.
(Ⅰ)写出曲线C和直线的普通方程;
(Ⅱ)若![]() 成等比数列,求a的值.
成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( ) 
A.35
B.20
C.18
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的正四棱锥P-ABCD中,O为底面正方形的重心,M,N分别为侧棱PA,PB的中点,有下列结论:
①PC∥平面OMN;
②平面PCD∥平面OMN;
③OM⊥PA;
④直线PD与直线MN所成角的大小为90°.
其中正确结论的序号是______.(写出所有正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com