
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个. |
分析 ①AC⊥BE,可由线面垂直证两线垂直;
②EF∥平面ABCD,可由线面平行的定义请线面平行;
③三棱锥A-BEF的体积为定值,可证明棱锥的高与底面积都是定值得出体积为定值,根据等积法可得答案;
④异面直线AE、BF所成的角为定值,可由两个极好位置说明两异面直线所成的角不是定值
解答 解:①AC⊥BE,由题意及图形知,AC⊥面DD1B1B,故可得出AC⊥BE,此命题正确;
②EF∥平面ABCD,由正方体ABCD-A1B1C1D1的两个底面平行,EF在其一面上,故EF与平面ABCD无公共点,故有EF∥平面ABCD,此命题正确;
③三棱锥A-BEF的体积为定值,由几何体的性质及图形知,三角形BEF的面积是定值,A点到面DD1B1B距离是定值,故可得三棱锥A-BEF的体积为定值,
又由△AEF的面积为定值,可得点B到平面AEF的距离为定值,此命题正确;
④异面直线AE、BF所成的角为定值,由图知,当F与B1重合时,令上底面顶点为O,则此时两异面直线所成的角是∠A1AO,当E与D1重合时,此时点F与O重合,则两异面直线所成的角是OBC1,此二角不相等,故异面直线AE、BF所成的角不为定值.
综上知①②③正确
故选:B.
点评 本题考查棱柱的结构特征,解答本题关键是正确理解正方体的几何性质,且能根据这些几何特征,对其中的点线面和位置关系作出正确判断.熟练掌握线面平行的判断方法,异面直线所成角的定义以及线面垂直的证明是解答本题的知识保证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 意向 | 男 | 女 | 合计 |
| 生 | 40 | 20 | 60 |
| 不生 | 20 | 20 | 40 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 |
| P | 0.5 | x | y |
| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{33}{64}$ | D. | $\frac{55}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
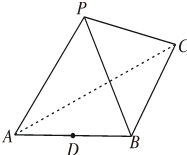 在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.
在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1] | D. | {-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com