
科目:高中数学 来源: 题型:
已知等差数列{an}满足a2013+a2015=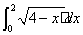 ,那么a2014(a2012+2a2014+a2016)的值为 ( )
,那么a2014(a2012+2a2014+a2016)的值为 ( )
A. B.2 C.² D.4²
查看答案和解析>>
科目:高中数学 来源: 题型:
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为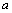 的平行线,将一根长度为
的平行线,将一根长度为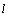 的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率
的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率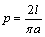 (
(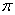 为圆周率).
为圆周率).
已知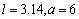 ,
,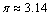 ,现随机掷14根相同的针(长度为
,现随机掷14根相同的针(长度为 )在这个平面上,记这些针与平行线(间距为
)在这个平面上,记这些针与平行线(间距为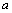 )相交的根数为
)相交的根数为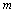 ,其相应的概率为
,其相应的概率为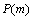 .当
.当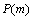 取得最大值时,
取得最大值时,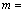 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线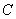 的极坐标方程为
的极坐标方程为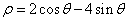 .以极点为原点,极轴为
.以极点为原点,极轴为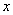 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为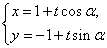 (
(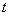 为参数).
为参数).
(Ⅰ)判断直线 与曲线
与曲线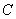 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)若直线 和曲线
和曲线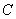 相交于
相交于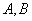 两点,且
两点,且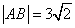 ,求直线
,求直线 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com