
| A. | -$\frac{11}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{11}{3}$ |
分析 可作出图形,根据$\overrightarrow{CM}=2\overrightarrow{MB}$便可得到$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$,根据条件$∠A=\frac{π}{3}$,AB=2,AC=3进行数量积的运算便可求出$(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})•(\overrightarrow{AC}-\overrightarrow{AB})$的值,从而得出$\overrightarrow{AM}•\overrightarrow{BC}$的值.
解答 解:如图,
$\overrightarrow{CM}=2\overrightarrow{MB}$;
∴$\overrightarrow{AM}-\overrightarrow{AC}=2(\overrightarrow{AB}-\overrightarrow{AM})$;
∴$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$;
∴$\overrightarrow{AM}•\overrightarrow{BC}=(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})•(\overrightarrow{AC}-\overrightarrow{AB})$
=$\frac{1}{3}\overrightarrow{AB}•\overrightarrow{AC}-\frac{2}{3}{\overrightarrow{AB}}^{2}+\frac{1}{3}{\overrightarrow{AC}}^{2}$
=$\frac{1}{3}×2×3×\frac{1}{2}-\frac{2}{3}×{2}^{2}+\frac{1}{3}×{3}^{2}$
=$\frac{4}{3}$.
故选:C.
点评 考查向量减法的几何意义,向量的数乘运算,以及向量数量积的运算及其计算公式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<2} | B. | {x|-1<x<1} | C. | {x|x≤1} | D. | {x|x>2} |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
六个面都是平行四边形的四棱柱称为平行六面体.如图甲,在平行四边形ABCD中,有AC2+BD2=2(AB2+AD2),那么在图乙所示的平行六面体ABCD-A1B1C1D1中, 等于( )
等于( )
A.2(AB2+AD2+ )
)
B.3(AB2+AD2+ )
)
C.4(AB2+AD2+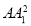 )
)
D.4(AB2+AD2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com