练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若a＞2010，0＜b＜1，则logab+logba的取值范围是
     
    ．
    考点：对数的运算性质
    专题：函数的性质及应用
    分析：由已知条件推导出∴logab＜0，logab+logba=-（-logab-
    1
    logab
    ），由此利用均值定理能求出结果．
    解答： 解：∵若a＞2010，0＜b＜1，
    ∴logab＜0，
    ∴logab+logba=-（-logab-
    1
    logab
    ）
    ≤-2
    		(-logab)(-
    1
    logab
    )

    =-2．
    当且仅logab=-1时，取等号，
    ∴logab+logba的取值范围是（-∞，-2]．
    故答案为：（-∞，-2]．
    点评：本题考查对数和的取值范围的求法，是基础题，解题时要注意对数的运算性质和运算法则的合理运用，注意均值定理的合理运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

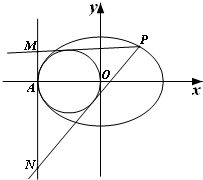    如图，离心率为
    		2
    2
    的椭圆
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）与直线l：x=-2相切于点A（-2，0）．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）若OA是圆C的直径，P（x0，y0）（x0＞0）为椭圆上的动点，过P作圆C的两条切线，分别交直线l于点M、N，求当
    PM
    •
    PN
    取得最小值时P点的横坐标x0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

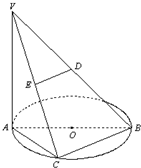    如图，AB是圆O的直径，点C是弧AB的中点，D，E分别是VB，VC的中点，VA⊥平面ABC．
    （1）求异面直线DE与AB所成的角；
    （2）证明：DE⊥平面VAC．
    （3）若AB=
    		2
    VA    ，求二面角A-BC-D的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在如图所示的正方体ABCD-A1B1C1D1中，E、F分别为棱AB与AA1的中点，则直线EF与平面ACC1A1成角的大小为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知F1、F2是椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的两个焦点，P为椭圆C上一点，且
    PF1
    ⊥
    PF2
    ．若△PF1F2的面积为16，则b=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    曲线
    x2
    25λ
    -
    y2
    16λ
    =1（λ≠0）的渐近线方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=a+log3x的图象过点A（1，1），则a=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

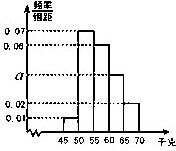    为了了解学生的身体状况，某校随机抽取了一批学生测量体重，经统计，这批学生的体重数据（单位为千克）全部介于45至70之间，将数据分成以下5组：第1组[45，50），第2组[50，55），第3组[55，60），第4组[60，65），第5组[65，70），得到如图所示的频率分布直方图，则a=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    圆（x-2）2+（y-1）2=4被双曲线
    x2
    9
    -
    y2
    16
    =1的一条渐近线截得的弦长为（　　）
    A、2
    		3
    B、2
    C、
    		3
    D、1

    查看答案和解析>>

    同步练习册答案