
���� ��1������f��x��������ת��Ϊy=m��y=f��x����x��[$\frac{��}{12}$��$\frac{��}{2}$]��2����ͬ�Ľ��㣬����������ͼ�����m�ķ�Χ���ɣ�
��2�����B��ֵ���������Ҷ����õ�a+c=2b=4���������Ҷ����õ�b2=a2+c2-2accosB=��a+c��2-2ac-$\sqrt{3}$ac�����ac��ֵ���Ӷ���������ε�������ɣ�
���  �⣺��1���ߺ���f��x��=$\frac{\sqrt{3}}{2}$sin2x-cos2x+$\frac{1}{2}$��
�⣺��1���ߺ���f��x��=$\frac{\sqrt{3}}{2}$sin2x-cos2x+$\frac{1}{2}$��
��f��x��=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1+cos2x}{2}$+$\frac{1}{2}$=sin��2x-$\frac{��}{6}$����
��f��x��=sin��2x-$\frac{��}{6}$����
��x��[$\frac{��}{12}$��$\frac{��}{2}$]����2x-$\frac{��}{6}$��[0��$\frac{5��}{6}$]��
��?x��[$\frac{��}{12}$��$\frac{��}{2}$]��f��x��-m=0��������ͬ�ĸ���
��y=m��y=f��x����x��[$\frac{��}{12}$��$\frac{��}{2}$]��2����ͬ�Ľ��㣬
����������ͼ����ͼ��ʾ��
��
���ͼ���$\frac{1}{2}$��m��1��
��2����f��B��=$\frac{1}{2}$����ã�B=$\frac{��}{6}$��B=$\frac{��}{2}$��
��sinA��sinB��sinC�ɵȲ����У�������Ҷ�����a+c=2b=4��
��B=$\frac{��}{6}$����b2=a2+c2-2accosB=��a+c��2-2ac-$\sqrt{3}$ac��
��ac=��24-12$\sqrt{3}$����
��S��ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$��24-12$\sqrt{3}$����$\frac{1}{2}$=6-3$\sqrt{3}$��
���� ���⿼�������Ǻ����Ļ������Һ����������Լ����Ҷ��������Ҷ�����Ӧ�ã���һ���е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� |  | B�� |  | C�� |  | D�� | 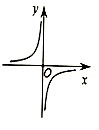 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����ij���дӸ߶��꼶�ס����������ָ�ѡ��7��ѧ���μ�2017��ȫ��������ѧ�������Ĵ�������������ȡ�õijɼ�������140�֣��ľ�Ҷͼ��ͼ��ʾ�����мװ�ѧ���ɼ�����λ����81���Ұ�ѧ���ɼ���ƽ������86������ʵ��a��b���㣺a��G��b�ɵȲ�������x��G��y�ɵȱ����У���$\frac{1}{a}$+$\frac{4}{b}$����СֵΪ��������
����ij���дӸ߶��꼶�ס����������ָ�ѡ��7��ѧ���μ�2017��ȫ��������ѧ�������Ĵ�������������ȡ�õijɼ�������140�֣��ľ�Ҷͼ��ͼ��ʾ�����мװ�ѧ���ɼ�����λ����81���Ұ�ѧ���ɼ���ƽ������86������ʵ��a��b���㣺a��G��b�ɵȲ�������x��G��y�ɵȱ����У���$\frac{1}{a}$+$\frac{4}{b}$����СֵΪ��������| A�� | $\frac{4}{9}$ | B�� | 2 | C�� | $\frac{9}{4}$ | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Sn=2n-2 | B�� | Sn=2n+1-2-n | C�� | Sn=2n-1-n | D�� | Sn=2n-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{5}{2}$ | B�� | $-\frac{9}{2}$ | C�� | $-\frac{11}{2}$ | D�� | $-\frac{13}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�պ�5�� | B�� | 5�պ�6�� | C�� | 6�պ�11�� | D�� | 4�պ�11�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com