Question

10．已知圆E：（x+$\sqrt{2}$）²+y²=12，点F（$\sqrt{2}$，0），点P为圆E上的动点，线段PF的垂直平分线交半径PE于点M．直线l：y=kx+m交椭圆于不同的两点A，B，原点O到直线l的距离为$\frac{\sqrt{3}}{2}$．
（Ⅰ）求动点M的轨迹方程；
（Ⅱ）求△OAB面积的最大值．

Answer 1

分析 （Ⅰ）由垂直平分线的性质可得|MP|=|MF|，根据图象和半径列出|ME|+|MP|=|EP|=4，由椭圆的定义判断出动点M的轨迹Γ是椭圆，求出基本量即可求出动点M的轨迹Γ方程；
（Ⅱ）由已知距离故选得到m，k的关系．将y=kx+m代入椭圆方程，整理得（1+3k²）x²+6kmx+3m²-3=0．然后根据根的判别式和根与系数的关系进行求解．

解答 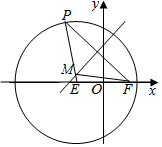解：（Ⅰ）由垂直平分线的性质可得|MP|=|MF|，如图：则|ME|+|MF|=|ME|+|MP|=|EP|=2$\sqrt{3}$＞2$\sqrt{2}$=|EF|，
∴动点M的轨迹Γ是以E，F为焦点，长轴长为2$\sqrt{3}$的椭圆．
可知a=$\sqrt{3}$，c=$\sqrt{2}$，故b=$\sqrt{{a}^{2}-{c}^{2}}$=1，
∴点M的轨迹Γ的方程为 $\frac{{x}^{2}}{3}+{y}^{2}=1$；
（Ⅱ）由已知直线l：y=kx+m交椭圆于不同的两点A，B，原点O到直线l的距离为$\frac{\sqrt{3}}{2}$．
可得：$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{3}}{2}$，可得m²=$\frac{3}{4}$（k²+1）．
将y=kx+m代入椭圆方程，整理得（1+3k²）x²+6kmx+3m²-3=0．
△=（6km）²-4（1+3k²）（3m²-3）＞0（*）
∴x₁+x₂=$\frac{-6km}{1+3{k}^{2}}$，x₁•x₂=$\frac{3{m}^{2}-3}{1+3{k}^{2}}$．
∴|AB|²=（1+k²）（x₂-x₁）²=（1+k²）[$\frac{36{k}^{2}{m}^{2}}{（1+3{k}^{2}）^{2}}$-$\frac{12（{m}^{2}-1）}{3{k}^{2}+1}$]
=$\frac{12（{k}^{2}+1）（3{k}^{2}+1-{m}^{2}）}{（1+3{k}^{2}）}$=$\frac{3（{k}^{2}+1）（9{k}^{2}+1）}{（3{k}^{2}+1）^{2}}$
=3+$\frac{12{k}^{2}}{9{k}^{4}+6{k}^{2}+1}$=3+$\frac{12}{9{k}^{2}+\frac{1}{{k}^{2}}+6}$≤3+$\frac{12}{2×3+6}$=4（k≠0）．
当且仅当$9{k}^{2}=\frac{1}{{k}^{2}}$，即k=±$\frac{\sqrt{3}}{3}$时等号成立．
经检验，k=±$\frac{\sqrt{3}}{3}$满足（*）式．
当k=0时，|AB|=$\sqrt{3}$．
综上可知|AB|_max=2．∴当|AB|最大时，△AOB的面积取最大值S=$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$．

点评 本题综合考查直线和椭圆的位置关系，难度较大，解题时要综合运用椭圆的性质，需要熟练地掌握公式的灵活运用．