
| A. | $-\frac{1}{4}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 根据题意,由函数的周期性以及奇偶性分析可得$f({-\frac{5}{2}})$=-f($\frac{5}{2}$)=-f($\frac{1}{2}$),又由函数在解析式可得f($\frac{1}{2}$)的值,综合可得答案.
解答 解:根据题意,f(x)是定义在R上周期为2的奇函数,则$f({-\frac{5}{2}})$=-f($\frac{5}{2}$)=-f($\frac{1}{2}$),
又由当0≤x≤1时,f(x)=x2-x,
则f($\frac{1}{2}$)=($\frac{1}{2}$)2-($\frac{1}{2}$)=-$\frac{1}{4}$,
则$f({-\frac{5}{2}})$=$\frac{1}{4}$,
故选:C.
点评 本题考查函数的值的计算,涉及函数的奇偶性与周期性的应用,属于基础题目.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{4}{9}$) | B. | [0,$\frac{1}{3}$) | C. | (-2,0) | D. | ($\frac{1}{3}$,$\frac{4}{9}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在(0,$\frac{π}{4}$)上单调递减 | B. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递减 | ||
| C. | f(x)在(0,$\frac{π}{4}$)上单调递增 | D. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (2,+∞] | C. | (0,2) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BO}=-\frac{5}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$ | B. | $\overrightarrow{BO}=\frac{1}{6}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$ | C. | $\overrightarrow{BO}=\frac{5}{6}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}$ | D. | $\overrightarrow{BO}=-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
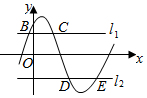 (理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )
(理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )| A. | 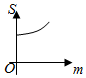 | B. | 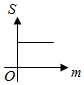 | C. | 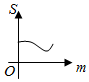 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [1,2) | C. | (1,2] | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com