
分析 (Ⅰ)先求出直线l的直角坐标方程,由此能求出直线l的极坐标方程;由曲线C的极坐标方程,能求出曲线C的直角坐标方程.
(Ⅱ)由直线l'与直线l平行,M(1,0)在直线l'上,能求出直线l'的参数方程,将它代入曲线C的方程得$5{t^2}+4t-12=0,{t_1}+{t_2}=-\frac{4}{5},{t_1}{t_2}=-\frac{12}{5}$,由此能求出|AB|.
解答 解:(Ⅰ)直线l的直角坐标方程为$y=\sqrt{3}({x-1})+1$,
所以直线l的极坐标方程为$ρsinθ=\sqrt{3}ρcosθ-\sqrt{3}+1$
又因为曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12,
所以曲线C的直角坐标方程为3x2+4y2=12,化简得$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)因为直线l'与直线l平行,
又M(1,0)在直线l'上,∴直线l'的参数方程为$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$,(t为参数),
将它代入曲线C的方程中得$5{t^2}+4t-12=0,{t_1}+{t_2}=-\frac{4}{5},{t_1}{t_2}=-\frac{12}{5}$,
所以$|{AB}|=|{{t_1}-{t_2}}|=\sqrt{{{({{t_1}+{t_2}})}^2}-4{t_1}{t_2}}=\sqrt{\frac{256}{25}}=\frac{16}{5}$.
点评 本题考查直线的极坐标方程、曲线的直角坐标方程的求法,考查弦长的求法,考查直角坐标方程、极坐标方程、参数方程的互化,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
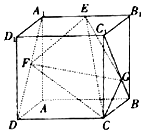 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
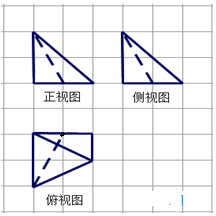 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
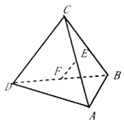 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )| A. | 120° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com