
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上递增,在
上递增,在![]() 上递减;(2)
上递减;(2)![]() .
.
【解析】试题分析:(1)1)当![]() 时,
时,![]() ,在
,在![]() 上单调递减; 2)当
上单调递减; 2)当![]() 时,
时,![]() .①当
.①当![]() 时,
时,![]() ,
,![]() 单调递减;②当
单调递减;②当![]() 时,
时,![]() 在
在![]() 上大于0,
上大于0,![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上小于0,
上小于0,![]() 在
在![]() 上单调递减;
上单调递减;
(2)①当![]() 时,
时,![]() ,满足题意;②当
,满足题意;②当![]() 时,
时,![]() ,不满足题意;③当
,不满足题意;③当![]() 时,
时,![]() ,不满足题意;④当
,不满足题意;④当![]() 时,由(1)可知
时,由(1)可知![]()
![]() 令
令![]() ,则将上式写为
,则将上式写为![]() ,令
,令![]() ,解得
,解得![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() 满足题意;当
满足题意;当![]() 时,
时,![]() ,
,![]() ,
,![]() 不满足题意;综上可得,当
不满足题意;综上可得,当![]() 时,
时,![]() .
.
试题解析:(1)1)当![]() 时,
时,![]() ,在
,在![]() 上单调递减;
上单调递减;
2)当![]() 时,
时,![]() .
.
①当![]() 时,在定义域
时,在定义域![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
②当![]() 时,
时,![]() 的解为
的解为![]() ,
,![]() (负值舍去),
(负值舍去),
![]() 在
在![]() 上大于0,
上大于0,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上小于0,
上小于0,![]() 在
在![]() 上单调递减;
上单调递减;
综上所述,当![]() 时,
时,![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)①当![]() 时,
时,![]() ,满足题意;
,满足题意;
②当![]() 时,
时,![]()
![]() ,不满足题意;
,不满足题意;
③当![]() 时,
时,![]() ,
,
由于![]() 且
且![]() ,
,
所以![]() 为两负数的乘积大于0,即
为两负数的乘积大于0,即![]() ,不满足题意;
,不满足题意;
④当![]() 时,由(1)可知
时,由(1)可知![]()
![]()
令![]() ,则将上式写为
,则将上式写为![]() ,令
,令![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
而当![]() 时,
时,![]() ,
,![]() ,
,![]() 满足题意;
满足题意;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 不满足题意;
不满足题意;
综上可得,当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
(1)求椭圆的方程;
(2)点![]() 为椭圆上的一动点(非长轴端点),
为椭圆上的一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点, ![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:
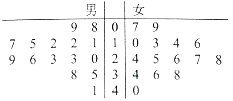
若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人?
(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人,参加读书日宣传活动.
(i)共有多少种不同的抽取方法?
(ii)求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝店经过对春节七天假期的消费者进行统计,发现在金额不超过1000元的消费者中男女比例为![]() ,该店按此比例抽取了100名消费者进行进一步分析,得到下表女性消费情况:
,该店按此比例抽取了100名消费者进行进一步分析,得到下表女性消费情况:
消费金额(元) |
|
|
|
|
|
人数 | 5 | 10 | 15 | 47 | 3 |
男性消费情况:
消费金额(元) |
|
|
|
|
|
人数 | 2 | 3 | 10 | 3 | 2 |
若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”
(1)分别计算女性和男性消费的平均数,并判断平均消费水平高的一方“网购达人”出手是否更阔绰?
(2)根据以上统计数据填写如下![]() 列联表,并回答能否在犯错误的概率不超过
列联表,并回答能否在犯错误的概率不超过![]() 的前提下认为“是否为‘网购达人’与性别有关”.
的前提下认为“是否为‘网购达人’与性别有关”.
女性 | 男性 | 合计 | |
“网购达人” | |||
“非网购达人” | |||
合计 |
附:  .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是:( )
A. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
B. 命题“存在![]() ,使得
,使得![]() ”的否定是:“任意
”的否定是:“任意![]() ,都有
,都有![]() ”
”
C. 若命题“非![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题
一定是真命题
D. 命题“若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知点A(﹣1,﹣2)和B(﹣3,6),直线l经过点P(1,﹣5).且与直线AB平行,求直线l的方程
(2)求垂直于直线x+3y﹣5=0,且与点P(﹣1,0)的距离是 ![]() 的直线m的方程.
的直线m的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com