
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
分析 先画出图形,设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,求出P,F2,A,B四点的坐标,从而根据PF2∥AB即可得${k}_{P{F}_{2}}={k}_{AB}$,从而可得到b=2c,根据a2=b2+c2即可得出$a=\sqrt{5}c$,从而得到该椭圆的离心率$\frac{c}{a}$.
解答 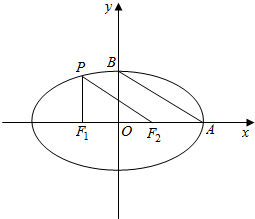 解:如图,
解:如图,
设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$;
∴x=-c时,${y}^{2}=\frac{{b}^{4}}{{a}^{2}}$,∴$P(-c,\frac{{b}^{2}}{a})$,F2(c,0);
又A(a,0),B(0,b),PF2∥AB;
∴${k}_{P{F}_{2}}={k}_{AB}$;
∴$-\frac{{b}^{2}}{2ac}=-\frac{b}{a}$;
∴b=2c;
$a=\sqrt{{b}^{2}+{c}^{2}}=\sqrt{5}c$;
∴$\frac{c}{a}=\frac{\sqrt{5}}{5}$;
即椭圆的离心率为:$\frac{\sqrt{5}}{5}$.
故选D.
点评 考查椭圆的标准方程,根据椭圆标准方程可表示椭圆的焦点及顶点坐标,根据椭圆的方程,已知椭圆上点的横坐标能求其纵坐标,根据两点坐标求直线斜率,以及两平行直线的斜率关系,椭圆离心率的概念及计算.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3{x^2}}}{25}-\frac{{3{y^2}}}{100}=1$ | B. | $\frac{{3{x^2}}}{100}-\frac{{3{y^2}}}{25}=1$ | ||
| C. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | D. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
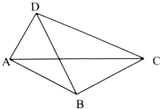
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有99%的人认为该栏目优秀 | |
| B. | 有99%的人认为该栏目是否优秀与改革有关系 | |
| C. | 有99%的把握认为电视栏目是否优秀与改革有关系 | |
| D. | 没有理由认为电视栏目是否优秀与改革有关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
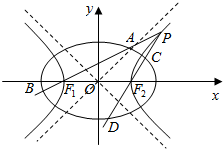 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<$\frac{1}{2}$且x≠-$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|x≤$\frac{1}{2}$且x≠-$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com