
分析 (1)当k=2时,甲总得分ξ的可能取值为2,3,4,分别求出相应的概率,由此能求出甲总得分ξ的分布列;乙总得分η的可能取值为2,3,4,分别求出相应的概率,由此能求出乙总得分η的分布列.
(2)当k=2时,甲总得分比乙总得分高的概率为P(ξ>η)=P(ξ=3)P(η=2)+P(ξ=4)P(η=2)+P(ξ=4)P(η=3);当k=1时,甲总得分比乙总得分高的概率为P(ξ>η)=P(ξ=4)P(η=3);当k=3时,甲总得分比乙总得分高的概率为P(ξ>η)=P(ξ=3)P(η=2)+P(ξ=4).由此能求出当k=2时甲总得分比乙总得分高的概率达到最大.
解答 解:(1)当k=2时,甲总得分ξ的可能取值为2,3,4,
P(ξ=2)=($\frac{2}{4}$)2=$\frac{1}{4}$,
P(ξ=3)=${C}_{2}^{1}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{2}$,
P(ξ=4)=($\frac{2}{4}$)2=$\frac{1}{4}$.
∴甲总得分ξ的分布列为:
| ξ | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
| η | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{2}{3}$ | $\frac{1}{6}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,考查推理论证能力、运算求解能力,考查函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为$\frac{{\sqrt{2}}}{10}$,$\frac{{2\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为$\frac{{\sqrt{2}}}{10}$,$\frac{{2\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-12,8) | B. | (-8,12) | C. | (-13,17) | D. | (-17,13) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
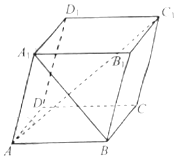 已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.
已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com