
分析 由条件利用三角恒等变换化简所给的式子可得结果.
解答 解:[2sin50°+sin10°(1+$\sqrt{3}$tan10°)]•$\sqrt{2si{n}^{2}80°}$
=[2sin50°+sin10°•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$]•$\sqrt{2}$cos10°
=[2sin50°+2sin10°•$\frac{\frac{1}{2}cos10°+\frac{\sqrt{3}}{2}sin10°}{cos10°}$]•$\sqrt{2}$cos10°
=2$\sqrt{2}$[sin50°cos10°+sin10°•cos(60°-10°)]=2$\sqrt{2}$sin(50°+10°)
=2$\sqrt{2}$sin60°=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题主要考查三角恒等变换,属于中档题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | 2-21-n | B. | 2n-1 | C. | 1 | D. | n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
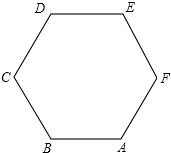
| A. | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B. | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D. | $\overrightarrow{CD}$•($\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$)=-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
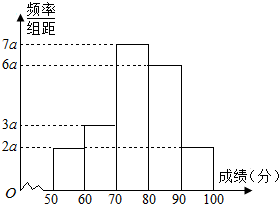 某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)
某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com