
| ����x����Ԫ�� | 8 | 8.2 | 8.4 | 8.8 | 8.6 | 9 |
| ����y������ | 90 | 84 | 83 | 75 | 80 | 68 |
���� ��1���ٸ��ݹ�ʽ���$\widehat{b}$��$\widehat{a}$��ֵ������ع鷽�̼��ɣ��ڸ���b��ֵ�жϼ��ɣ���2���������w�ı���ʽ����϶��κ������������w�����ֵ���ɣ�
��� �⣺��1���������⣺$\stackrel{��}{b}$=$\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y��}}}{{\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}}}$=-20��
$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$=80+20��8.5=250��
��ع�ֱ�ߵķ���Ϊy=-20x+250��
������$\widehat{b}$=-20��0����x��y����أ�
���涨�۵����ӣ��������Ͻ��ͣ�
��2�����������������Ϊw���趨��Ϊx��
��w=��x-4.5����-20x+250��=-20x2+340x-1125��
�൱$x=\frac{340}{40}=8.5$ʱ��wmax=320��
�ʵ�����Ϊ8.5Ԫʱ��wȡ�����ֵ��
���� ���⿼���˻ع鷽�����⣬������κ��������ʣ���һ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪F1��F2�ֱ�Ϊ��ԲC1��$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1��a��b��0�����ϡ��½��㣬����F1Ҳ��������C2��x2=4y�Ľ��㣬��M��C1��C2�ڵڶ����Ľ��㣬��|MF1|=$\frac{5}{3}$��
��֪F1��F2�ֱ�Ϊ��ԲC1��$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1��a��b��0�����ϡ��½��㣬����F1Ҳ��������C2��x2=4y�Ľ��㣬��M��C1��C2�ڵڶ����Ľ��㣬��|MF1|=$\frac{5}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
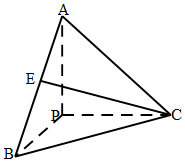 ��֪��ͼ��PA��PB��PC���ഹֱ���ҳ�����ȣ�EΪAB�е㣬��ֱ��CE��ƽ��PAC���ɽǵ�����ֵΪ$\frac{\sqrt{6}}{6}$��
��֪��ͼ��PA��PB��PC���ഹֱ���ҳ�����ȣ�EΪAB�е㣬��ֱ��CE��ƽ��PAC���ɽǵ�����ֵΪ$\frac{\sqrt{6}}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a����b������a��b | B�� | ��a����b�֣�a��b������� | ||
| C�� | ��a�ͦ���a?�£�����ͦ� | D�� | ��a��b�ڦ��ڵ���Ӱ���ֱ����a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {5��7} | B�� | {1��3��9} | C�� | {3��5��7} | D�� | {1��2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com