
 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,$BD=2\sqrt{3}$,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,$BD=2\sqrt{3}$,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.分析 (1)易知O为BD的中点,则AC⊥BD,即AC⊥平面PBD,即平面PAC⊥平面PDB.
(2)过P作DB的垂线,垂足为H,则PH垂直平面ABCD,∠PHO=60°,
以OB为x后,OC为y轴,过O垂直于平面ABC向上的直线为z轴建立如图所示空间直角坐标系,利用向量法求解.
解答 解:(1)证明:∵△BCD为正三角形,AD=AB=2,易知O为BD的中点,则AC⊥BD,
又PO?平面PBD,所以AC⊥平面PBD,∵AC?平面PAC,∴平面PAC⊥平面PDB.
(2)过P作DB的垂线,垂足为H,则PH垂直平面ABCD,∠PHO=60°,
以OB为x后,OC为y轴,过O垂直于平面ABC向上的直线为z轴建立如图所示空间直角坐标系,
则A(0,-1,0),$B(\sqrt{3},0,0)$,$P(-\frac{{\sqrt{3}}}{2},0,\frac{3}{2})$,
易知平面PBD的法向量为$\overrightarrow n=(0,1,0)$,$\overrightarrow{AB}=(\sqrt{3},1,0)$,$\overrightarrow{AP}=(-\frac{{\sqrt{3}}}{2},1,\frac{3}{2})$,
设平面ABP的法向量为$\overrightarrow n=(x,y,z)$,
则由$\left\{{\begin{array}{l}{\overrightarrow n⊥\overrightarrow{AB}}\\{\overrightarrow n⊥\overrightarrow{AP}}\end{array}}\right.$得$\left\{{\begin{array}{l}{\overrightarrow n×\overrightarrow{AB}=\sqrt{3}x+y=0}\\{\overrightarrow n×\overrightarrow{AP}=-\frac{{\sqrt{3}}}{2}x+y+\frac{3}{2}z=0}\end{array}}\right.$,
取$\overrightarrow n=(1,-\sqrt{3},\sqrt{3})$,$cos<\overrightarrow m,\overrightarrow n>=\frac{{\sqrt{3}}}{{\sqrt{7}}}=\frac{{\sqrt{21}}}{7}$,
二面角A-PB-D的余弦值为$\frac{{\sqrt{21}}}{7}$.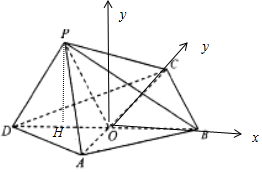
点评 本题考查了空间面面垂直的判定,向量法求空间角,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:选择题
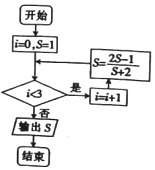
| A. | $-\frac{31}{15}$ | B. | $-\frac{7}{5}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{9}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
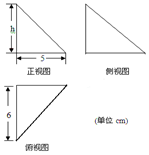 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )| A. | 55π | B. | 75π | C. | 77π | D. | 65π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=\sqrt{3}$ | B. | $a>\sqrt{3}$或$a<-\sqrt{3}$ | C. | $-\sqrt{3}<a<\sqrt{3}$ | D. | $-\sqrt{3}≤a≤\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
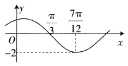 已知函数f(x)=Asin(wx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=Asin(wx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=2sin(2x-$\frac{π}{3}$) | B. | g(x)=2sin(2x+$\frac{π}{6}$) | C. | g(x)=-2sin(2x-$\frac{π}{3}$) | D. | g(x)=-2sin(2x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 济南 | B. | 青岛 | C. | 济南和潍坊 | D. | 济南和青岛 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
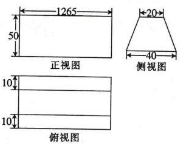 中国古代数学名著《九章算术》卷第五“商功”共收录28个题目,其中一个题目如下:今有城下广四丈,上广二丈,高五丈,袤一百二十六丈五尺,问积几何?其译文可用三视图来解释:某几何体的三视图如图所示(其中侧视图为等腰梯形,长度单位为尺),则该几何体的体积为( )
中国古代数学名著《九章算术》卷第五“商功”共收录28个题目,其中一个题目如下:今有城下广四丈,上广二丈,高五丈,袤一百二十六丈五尺,问积几何?其译文可用三视图来解释:某几何体的三视图如图所示(其中侧视图为等腰梯形,长度单位为尺),则该几何体的体积为( )| A. | 3795000立方尺 | B. | 2024000立方尺 | C. | 632500立方尺 | D. | 1897500立方尺 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com