
分析 (1)分类讨论,利用绝对值的几何意义得答案;
(Ⅱ)求出f(x)≤$\frac{{t}^{2}+4}{t}$对任意t>0的最小值,f(x)=|x-a|+|x-2|≥|x-a-x+2|=|a-2|,即f(x)的最小值为|a-2|.即可求得实数a的取值范围.
解答 解:(1)当a=1,f(x)=|x-1|+|x-2|.
不等式f(x)>2化为|x-1|+|x-2|≤2.
x<1时,不等式可化为3-2x≤2,∴x≥$\frac{1}{2}$,∴$\frac{1}{2}$≤x<1;
1≤x≤2时,不等式可化为1≤2,成立;
x>2时,不等式可化为2x-3≤2,∴x≤$\frac{5}{2}$,∴2<x≤$\frac{5}{2}$;
综上所述,不等式的解集为[$\frac{1}{2}$,$\frac{5}{2}$];
(2)f(x)=|x-a|+|x-2|≥|x-a-x+2|=|a-2|,即f(x)的最小值为|a-2|.
∵t>0,$\frac{{t}^{2}+4}{t}$=t+$\frac{4}{t}$≥4,当且仅当t=2时,$\frac{{t}^{2}+4}{t}$取得最小值4,
由题意,|a-2|≤4,∴-2≤a≤6.
点评 本题考查函数存在性问题,考查了绝对值不等式的解法,正确理解、运用绝对值的几何意义是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
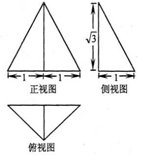
| A. | $\frac{\sqrt{3}}{3}$π | B. | π | C. | $\frac{26}{3}$π | D. | $\frac{32\sqrt{3}}{27}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,$BD=2\sqrt{3}$,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,$BD=2\sqrt{3}$,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(2x-\frac{π}{3}),x∈R$ | B. | $y=sin(\frac{x}{2}+\frac{π}{6}),x∈R$ | C. | $y=sin(2x+\frac{π}{3}),x∈R$ | D. | $y=sin(2x+\frac{2π}{3}),x∈R$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
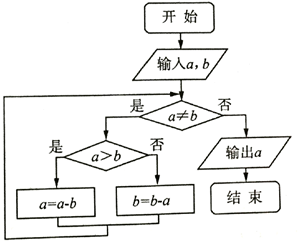 如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a=14,b=21,则输出的a=( )
如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a=14,b=21,则输出的a=( )| A. | 2 | B. | 3 | C. | 7 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
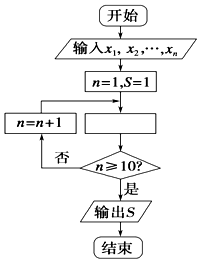
| A. | $S=S+\frac{x_n}{10}$ | B. | $S=S+\frac{x_n}{n}$ | C. | S=S+n | D. | S=S+xn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com